Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 1/3 + −2/5+ 1/6 + −1/5 ≤ x < −3/4+2/7+-1/4+3/5+5/7
⇒10-12+5-6/30≤ x< -105+40-35+84+100/140
⇒-3/30≤ x <84/140
⇒-0,1≤ x < 0,6
⇒x=0

\(A=\dfrac{3}{4}\cdot\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot...\cdot\dfrac{899}{900}\)
\(A=\dfrac{1\cdot3}{2\cdot2}\cdot\dfrac{2\cdot4}{3\cdot3}\cdot\dfrac{3\cdot5}{4\cdot4}\cdot...\cdot\dfrac{29\cdot31}{30\cdot30}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot...\cdot30\right)^2}\)
\(A=\dfrac{1\cdot\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot31}{\left(2\cdot3\cdot4\cdot5\cdot...\cdot29\right)^2\cdot30\cdot30}\)
\(A=\dfrac{1\cdot31}{30}=\dfrac{31}{30}\)
Ta có : \(\dfrac{1}{101}>\dfrac{1}{300}\)
...
\(\dfrac{1}{299}>\dfrac{1}{300}\)
Do đó :
\(\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{1}{300}+\dfrac{1}{300}..+\dfrac{1}{300}\)
\(\Rightarrow\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{300}>\dfrac{200}{300}=\dfrac{2}{3}\)
Vậy...

\(A=\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+...+\dfrac{1}{8}.\dfrac{1}{9}\)
\(=\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{8.9}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
\(=\dfrac{1}{2}-\dfrac{1}{9}\)
\(=\dfrac{7}{18}\)
\(B=\dfrac{1}{20}+\dfrac{1}{30}+...+\dfrac{1}{110}\)
\(=\dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{10.11}\)
\(=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
\(=\dfrac{1}{4}-\dfrac{1}{11}\)
\(=\dfrac{7}{44}\)

5, \(\dfrac{1}{7}.\dfrac{2}{5}+\dfrac{1}{7}.\dfrac{1}{5}+\dfrac{1}{7}.\dfrac{4}{5}\)
= \(\dfrac{1}{7}.\left(\dfrac{2}{5}+\dfrac{1}{5}+\dfrac{4}{5}\right)\)
= \(\dfrac{1}{7}\).1
=\(\dfrac{1}{7}\)
5) \(\dfrac{1}{7}.\dfrac{2}{5}+\dfrac{1}{7}.\dfrac{1}{5}+\dfrac{1}{7}.\dfrac{4}{5}\) = \(\dfrac{1}{7}.\left(\dfrac{2}{5}+\dfrac{1}{5}+\dfrac{4}{5}\right)\)
= \(\dfrac{1}{7}.\dfrac{7}{5}=\dfrac{1}{5}\)

a) \(1-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3-2}{6}=\dfrac{1}{6}\)
\(\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{5-4}{20}=\dfrac{1}{20}\)
\(\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{6-5}{30}=\dfrac{1}{30}\)
b) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{3}-\dfrac{1}{4}\right)+\left(\dfrac{1}{4}-\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)\)
\(=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{4}+\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+-\dfrac{1}{6}\)\(=1+-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)
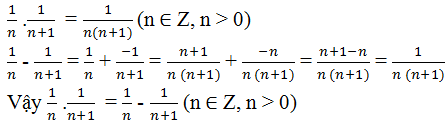

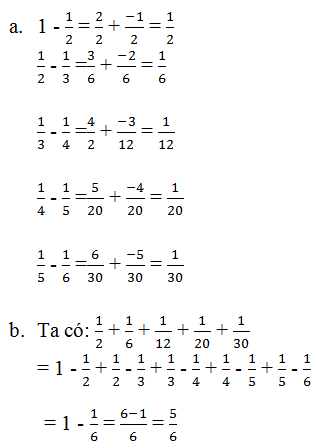


BT1: \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}>\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}>1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{5}{6}\)
Vậy ta suy ra đpcm
1. Ta có :
\(\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{6}>\dfrac{1}{6}+\dfrac{1}{6}+.....+\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{6}< \dfrac{1}{6}.5\)
\(\Leftrightarrow\dfrac{1}{2}+\dfrac{1}{3}+.....+\dfrac{1}{6}< \dfrac{5}{6}\)
\(\rightarrowđpcm\)