
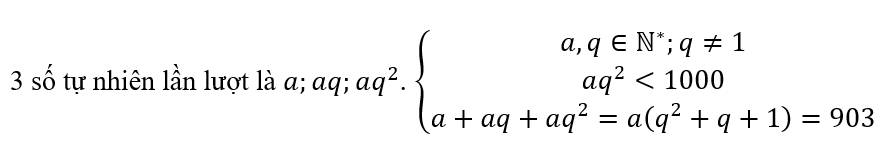
| \(a\) | 1 | 3 | 7 | 21 | 43 | 129 | 301 | 903 |
| \(q^2+q+1\) | 903 | 301 | 129 | 43 | 21 | 7 | 3 | 1 |
| \(q\) | x | x | x | 6 | 4 | 2 | 1 (loại) | x |
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

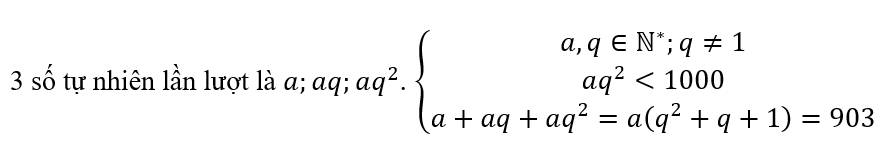
| \(a\) | 1 | 3 | 7 | 21 | 43 | 129 | 301 | 903 |
| \(q^2+q+1\) | 903 | 301 | 129 | 43 | 21 | 7 | 3 | 1 |
| \(q\) | x | x | x | 6 | 4 | 2 | 1 (loại) | x |
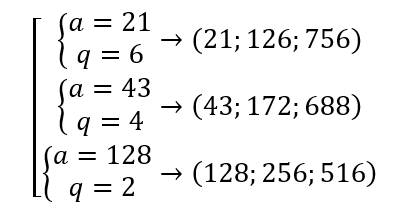

Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .

Chọn B
Giả sử ba số hạng a, b, c lập thành cấp số cộng thỏa yêu cầu, khi đó b, a, c theo thứ tự đó lập thành cấp số nhân công bội q. Ta có
a + c = 2 b a = b q ; c = b q 2 ⇒ b q + b q 2 = 2 b ⇔ b = 0 q 2 + q − 2 = 0 .
Nếu b = 0 ⇒ a = b = c = 0 nên a, b, c là cấp số cộng công sai d= 0 (vô lí).
Nếu q 2 + q − 2 = 0 ⇔ q = 1 hoặc q= -2. Nếu q = 1 ⇒ a = b = c (vô lí), do đó q = -2.

Đáp án A
Số cách chọn ra ngẫu nhiên 3 số từ A bằng C 100 3
Ta tìm số cách chọn ra bộ ba số thoả mãn:
Giả sử ba số chọn ra là
![]()
Ta có
![]()
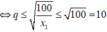
![]()
Mặt khác
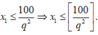
Với mỗi q ∈ 2 , 3 , . . . , 10 thì 100 q 2 cách chọn
và x 2 = q x 1 , x 3 = q 2 x 1 có tương ứng duy nhất một cách chọn.
Vậy theo quy tắc cộng và quy tắc nhân có tất cả
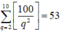
Xác suất cần tính bằng
53 C 100 3 = 53 161700

Ta có: \({S_n} = \frac{{5\left( {1 - {2^n}} \right)}}{{1 - 2}} = - 5 + 5 \times {2^n}\;\)
\(\begin{array}{l}5115 = - 5 + {5.2^n}\\ \Leftrightarrow {2^n} = 1024 = 2.\\ \Rightarrow n = 10.\end{array}\)
Vậy phải lấy tổng 10 số hạng đầu.