Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

R1ntR2
\(=>R1+R2=100\Omega\)(1)
R1//R2
\(=>R_{td}=\dfrac{R1.R2}{R1+R2}=\dfrac{R1.R2}{100}=16\)
=>R1.R2=1600(2)
Từ (1)(2)
=> R1=20 \(\Omega\)
R2=80\(\Omega\)

Ta có: R = 100\(\Omega\) > R' = 16\(\Omega\)
\(\Rightarrow\) R là điện trở tương đương của mạch mắc nối tiếp
R' là điện trở tương đương của mạch mắc song song
Ta có: R = R1 + R2 (R1 nối tiếp R2)
\(\Rightarrow\) R1 = 100 - R2
Ta có: R' = \(\dfrac{R_1.R_2}{R_1+R_2}\) (R1 song song R2)
\(\Rightarrow\) 16 = \(\dfrac{R_1.R_2}{100}\)
\(\Rightarrow\) R1 . R2 = 16 . 100
\(\Rightarrow\) R1 . R2 = 1600
\(\Rightarrow\) (100 - R2) . R2 = 1600
\(\Rightarrow\) 100R2 - R22 = 1600
\(\Rightarrow\) R22 - 100R2 + 1600 = 0
\(\Rightarrow\) R22 - 2 . R2 . 50 + 502 - 502 + 1600 = 0
\(\Rightarrow\) (R2 - 50)2 - 900 = 0
\(\Rightarrow\) (R2 - 50)2 - 302 = 0
\(\Rightarrow\) (R2 - 50 + 30) . (R2 - 50 - 30) = 0
\(\Rightarrow\) (R2 - 20) . (R2 - 80) = 0
\(\Rightarrow\) \(\left[{}\begin{matrix}R_2-20=0\\R_2-80=0\end{matrix}\right.\)
\(\Rightarrow\) \(\left[{}\begin{matrix}R_2=20\Rightarrow R_1=80\\R_2=80\Rightarrow R_1=20\end{matrix}\right.\)
trong hai trường hợp đó thì chỉ nối tiếp và song song thôi
R1+R2=100
\(\dfrac{R_1R_2}{R_1+R_2}\)=16
Từ hai phương trình đó thì bạn giải giùm mình nhé

1,th1:R1ntR2ntR3
Rtđ=6+6+6=18Ω
th2:R1//R2//R3
Rtđ=\(\frac{6}{3}\)=2Ω
th3:(R1ntR2)//R3
Rtđ=\(\frac{\left(6+6\right).6}{6+6+6}\)=4Ω
th4(R1//R2)ntR3
Rtđ=\(\frac{6}{2}\)+6=9Ω
2,ta có phương trình :
(R1+R2)=\(\frac{R_1R_2}{R1+R2}\).6,25
(R1+R2)2=R1R2.6,25
R12+2R1R2+R22=R1R2.6,25
R12-4,25R1R2+R22=0
(\(\frac{R1}{R2}\))2-4,25\(\frac{R1}{R2}\)+1=0
x2-4,25x+1=0 (x=\(\frac{R1}{R2}\))
x2-4x-0,25x+1=0
(x-0,25)(x-4)=0
x=\(\frac{R1}{R2}\)=(0,25;4)

a) Rtd= \(\frac{1}{R_1}+\frac{1}{R_2}\)= \(\frac{1}{15}+\frac{1}{10}\)=6 \(\Omega\)
b) I=\(\frac{U}{R}\)(định luật ôm)=\(\frac{18}{6}\)=3(A)

Đáng ra phải là chọn câu đúng chứ:
A. Điện trở tương đương R của n điện trở r mắc nối tiếp : R=n.r
B.điện trở tương đương R của n điện trở r mắc song song : R=rnrn
C.Điện trở tương đương của mạch mắc song song nhỏ hơn điện trở mỗi thành phần
D.Trong đoạn mạch mắc song song cường độ dòng điện chạy qua các điện trở là bằng nhau

a)Điện trở tương đương
Rtđ=R1+R2=15+30=45 (ôm)
b)CĐDĐ
I=U/R=15:45=0.3(A)

*Tóm tắt:
R1= 10Ω ; R2 = R3 = 20Ω
a) Rtđ = ?
b) I1 = 2,4A ; UAB = ? ; IAB = ? ; I2 = ? ; I3=?
__________________________________
Sơ đồ mạch điện bạn tự vẽ nha :)
a) Đoạn mạch gồm R1 // R2 // R3
Điện trở tương đương của đoạn mạch là:
\(\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{Rtđ}\)
=>\(\dfrac{1}{10}+\dfrac{1}{20}+\dfrac{1}{20}=\dfrac{1}{Rtđ}\)
=>\(\dfrac{1}{Rtđ}=\dfrac{1}{5}\)
=> Rtđ = 5Ω
b)Hiệu điện thế giữa 2 đầu đoạn mạch là :
UAB = U1 = I1.R1 = 2,4 . 10 = 24 (V)
Cường độ dòng điện chạy qua mạch chính là :
IAB = \(\dfrac{U_{AB}}{R_{tđ}}=\dfrac{24}{5}=4,8\left(A\right)\)
Cường độ dòng điện chạy qua mạch rẽ 2 và 3 là:
I2 = I3 = \(\dfrac{I_{AB}-I_1}{2}=\dfrac{4,8-2,4}{2}=1,2\left(A\right)\)
Đ/S:....


Biểu thức xác định điện trở tương đương của đoạn mạch có hai điện trở R1, R2 mắc song song: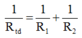
→ Đáp án A