Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5,25 5,42 5,98 6,68 6,21 6,81 7,08 7,02
b)
+) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5,25 5,42 5,98 6,21 6,68 6,81 7,02 7,08
+) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 7,08 - 5,25 = 1,83\)
c)
+) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5,25 5,42 5,98 6,21 6,68 6,81 7,02 7,08
+) Các tứ phân vị của mẫu số liệu là: \({Q_1} = 5,7,{Q_2} = 6,445,{Q_3} = 6,915\)
+) Khoảng tứ phân vị của mẫu số liệu là: \({Q_3} - {Q_1} = 1,215\)
d)
+) Tốc độ tăng trưởng GDP trung bình của Việt Nam giai đoạn 2012 – 2019 là:\(\overline x = \frac{{5,25{\rm{ + }}5,42{\rm{ + }}5,98{\rm{ + }}6,21{\rm{ + }}6,68\; + 6,81{\rm{ + }}7,02{\rm{ + }}7,08}}{8} = 6,30625\) (%)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5,25 - \overline x } \right)}^2} + {{\left( {5,42 - \overline x } \right)}^2} + ... + {{\left( {7,08 - \overline x } \right)}^2}} \right]}}{8} \approx 0,44\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} \approx 0,66\)(%)

Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)

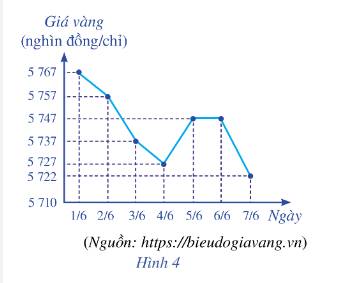
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757- 5727= 30.
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\)( nghìn đồng/ chỉ)

Chọn A.
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Số khách | 430 | 550 | 430 | 520 | 550 | 515 | 550 | 110 | 520 | 430 | 550 | 880 | Cộng: 6035 |
Đơn vị điều tra: Số khách đến tham quan một điểm du lịch trong 12 tháng
Kích thước mẫu của số liệu: 6035

Sắp xếp theo thứ tự không giảm.
2,593 2,977 3,155 3,270 3,387 3,412 3,813 3,920 4,042 4,236
Khoảng biến thiên \(R = 4,236 - 2,593 = 1,643\)
Vì n=10 nên ta có:
\({Q_1} = 3,155\); \({Q_3} = 3,920\)
Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 3,920 - 3,155\)\( = 0,765\)
\(\overline x \approx 3,481\)
Ta có:
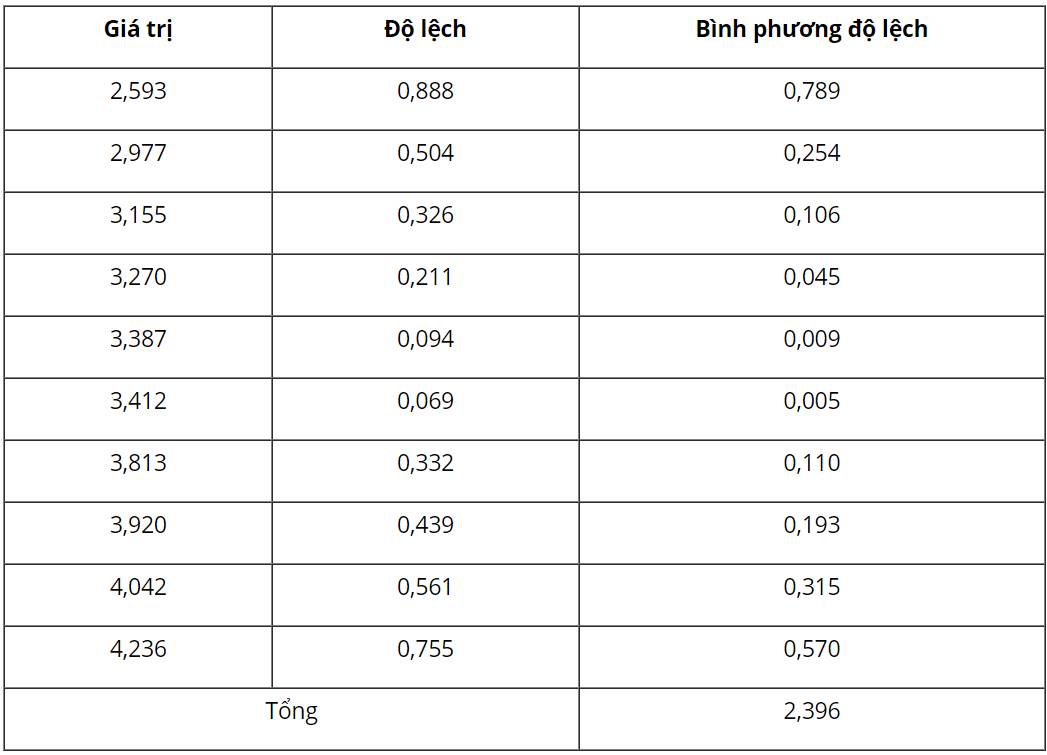
Độ lệch chuẩn: \(s = \sqrt {0,2396} \approx 0,489\)Phương sai là: \({s_2} = \frac{{2,396}}{{10}} = 0,2396\)

Tham khảo:
n=10
Giả sử sau khi sắp xếp 10 số dương theo thứ tự không giảm thì được:

=> Trung vị là giá trị trung bình của số thứ 5 và thứ 6.
=> \({Q_1}\) là số thứ 3 và \({Q_3}\) là số thứ 8.
a) Khi nhân mỗi giá trị của mẫu số liệu với 2 thì:
+ Số lớn nhất tăng 2 lần và số nhỏ nhất tăng 2 lần
=> R tăng 2 lần
+ \({Q_1}\) và \({Q_3}\) tăng 2 lần
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) tăng 2 lần.
+ Giá trị trung bình tăng 2 lần
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) cũng tăng 2 lần
=> \({\left( {{x_i} - \overline x} \right)^2}\) tăng 4 lần
=> Phương sai tăng 4 lần
=> Độ lệch chuẩn tăng 2 lần.
Vậy R tăng 2 lần, khoảng tứ phân vị tăng 2 lần và độ lệch chuẩn tăng 2 lần.
b) Cộng mỗi giá trị của mẫu số liệu với 2 thì
+ Số lớn nhất tăng 2 đơn vị và số nhỏ nhất tăng 2 đơn vị
=> R không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ \({Q_1}\) và \({Q_3}\) tăng 2 đơn vị
=> Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
+ Giá trị trung bình tăng 2 đơn vị
=> Độ lệch của mỗi giá trị so với giá trị trung bình \(\left| {{x_i} - \overline x} \right|\) không đổi vì phần tăng thêm bị triệt tiêu cho nhau.
=> \({\left( {{x_i} - \overline x} \right)^2}\) không đổi
=> Phương sai không đổi.
=> Độ lệch chuẩn không đổi.
Vậy khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn đều không đổi.

a) Sắp xếp theo thứ tự không giảm:
0 0 0 0 0 0 0 4 6 10
Số trung bình: \(\overline X = \dfrac{{0.7 + 4 + 6 + 10}}{{10}} = 2\)
Trung vị: \({Q_2} = 0\)
+ Mốt: 0
Tứ phân vị:
+ Nửa bên trái của \({Q_2}\):
0 0 0 0 0
=>\({Q_1} = 0\)
+ Nửa bên phải của \({Q_2}\):
0 0 4 6 10
=>\({Q_3} = 4\)
b) Tứ phân vị thứ nhất và trung vị trùng nhau vì mật độ của mẫu số liệu tập trung hết ở nửa trái của trung vị, mẫu số liệu bên trái có số liệu bằng 0 hết.

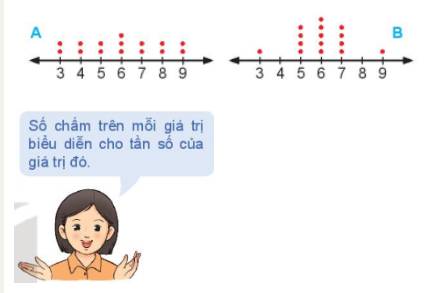
a) Cả 2 mẫu đều có n=15.
Ta có cả 2 mẫu đều có giá trị nhỏ nhất là 3, giá trị lớn nhất là 9
Do đó cả 2 mẫu cùng khoảng biến thiên.
Cả 2 biểu đồ này có dạng đối xứng nên giá trị trung bình của hai mẫu A và B bằng nhau.
b) Từ biểu đồ ta thấy, mẫu A có các số liệu đồng đều và ổn định hơn mẫu B nên phương sai của mẫu A nhỏ hơn mẫu B.
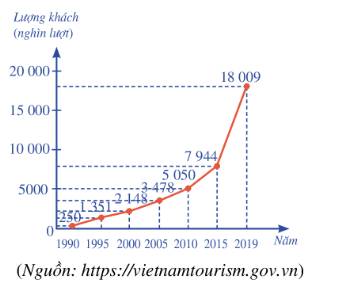

a) Mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên là:
250 1351 2148 3478 5050 7944 18009
b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: 250 1351 2148 3478 5050 7944 18009
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{250{\rm{ + }}1351{\rm{ + }}2148{\rm{ + }}3478{\rm{ + }}5050{\rm{ + }}7944{\rm{ + }}18009}}{7} = \frac{{38230}}{7}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 3478\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 250 1351 2148 là: \({Q_1} = 1351\)
- Trung vị của dãy 5050 7944 18009 là: \({Q_3} = 7944\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 1351\), \({Q_2} = 3478\), \({Q_3} = 7944\)
c) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 18009 - 250 = 17759\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 7944 - 1351 = 6593\)
d) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {250 - \overline x } \right)}^2} + {{\left( {351 - \overline x } \right)}^2} + ... + {{\left( {18009 - \overline x } \right)}^2}} \right]}}{7} \approx 31820198,82\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 5640,93\)