Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(\left\{{}\begin{matrix}2x-1\le0\\-3x+5< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{1}{2}\\x>\dfrac{5}{3}\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\).
b) Vẽ hai đường thẳng \(y=3;2x-3y+1=0\).
Vì điểm \(O\left(0;0\right)\) có tọa độ thỏa mãn bất phương trình \(2x-3y+1>0\) và không thỏa mãn bất phương trình \(3-y< 0\) nên phần không tô màu là miền nghiệm của hệ bất phương trình: \(\left\{{}\begin{matrix}3-y< 0\\2x-3y+1>0\end{matrix}\right.\).
TenAnh1
TenAnh1
A = (-4.34, -5.96)
A = (-4.34, -5.96)
A = (-4.34, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)
B = (11.02, -5.96)

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
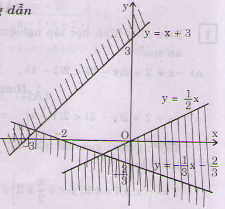
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
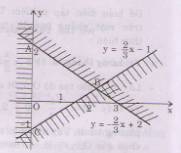

Tham khảo:
Bước 1: Xác định miền nghiệm của bất phương trình \(x \ge 0\)
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0).
Bước 2: Xác định miền nghiệm của bất phương trình \(y > 0\)
Miền nghiệm của bất phương trình \(y > 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) không kể trục Ox.
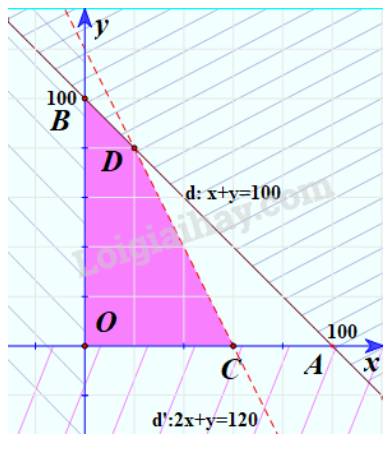
Bước 3: Xác định miền nghiệm của bất phương trình \(x + y \le 100\)
+ Vẽ đường thẳng d: x+y=100
+ Vì 0+0=0
Do đó, miền nghiệm của bất phương trình \(x + y \le 100\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Bước 4: Xác định miền nghiệm của bất phương trình \(2x + y < 120\)
Tương tự miền nghiệm của bất phương trình \(2x + y < 120\) là nửa mặt phẳng bờ d’ chúa gốc tọa độ O. (không kể đường thẳng d’).
Khi đó miền không bị gạch là giao của các miền nghiệm của các bất phương trình trong hệ. Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không kể đoạn thẳng OC và CD).

a)
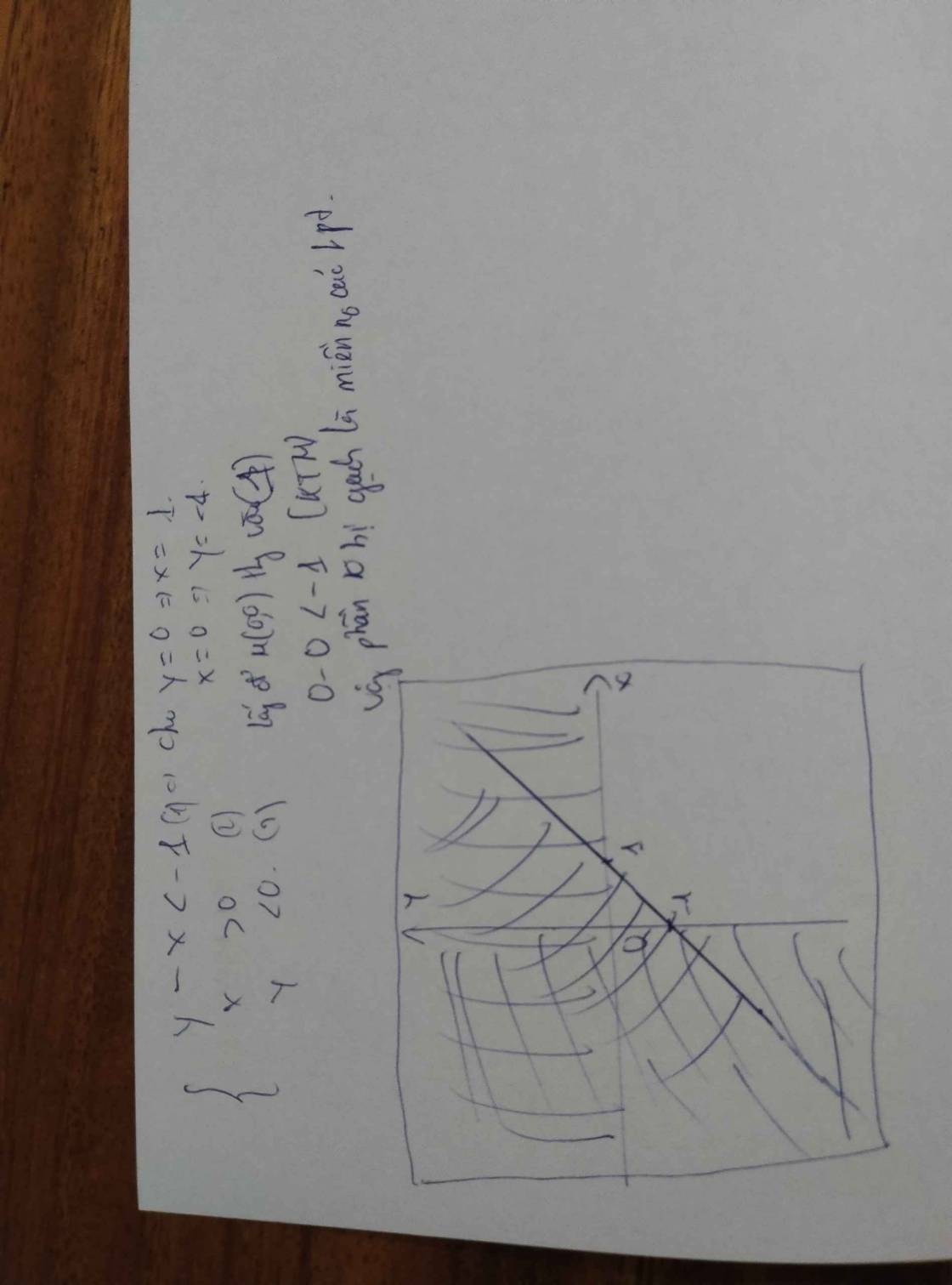
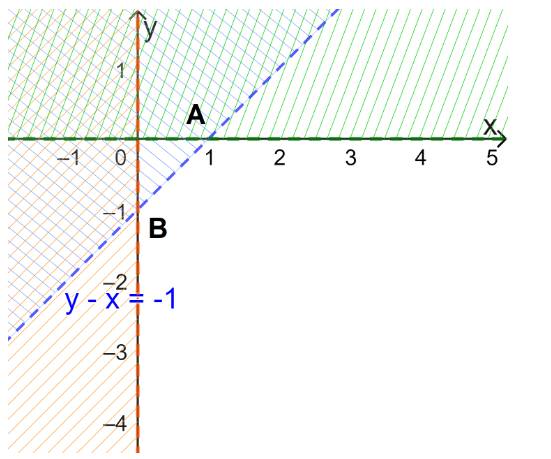
Xác định miền nghiệm của BPT \(y - x < - 1\)
+ Vẽ đường thẳng d: \(y-x= - 1\) đi qua A(1;0) và B(0;-1)
+ Vì \(0-0= 0 > - 1\) nên tọa độ điểm O(0;0) không thỏa mãn BPT \(y - x < - 1\)
Do đó, miền nghiệm của BPT \(y - x < - 1\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Miền nghiệm của BPT \(x > 0\) là nửa mặt phẳng bên phải Oy (không kể trục Oy).
Miền nghiệm của BPT \(y < 0\) là nửa mặt phẳng dưới Ox (không kể trục Ox).
Khi đó miền nghiệm của hệ bất phương trình đã cho là miền không gạch (Không kể đoạn thẳng AB và các trục tọa độ).
b)
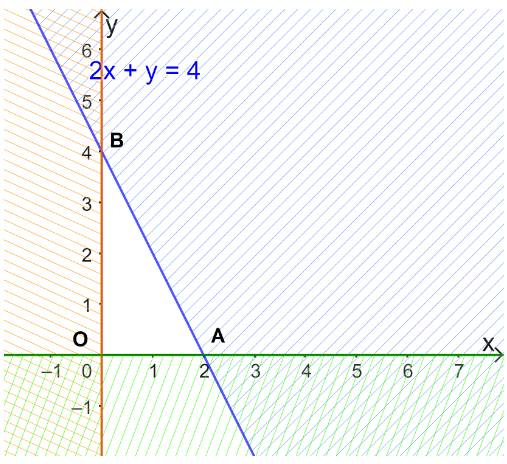
Miền nghiệm của BPT \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0) (kể cả trục Oy).
Miền nghiệm của BPT \(y \ge 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) (kể cả trục Ox).
Xác định miền nghiệm của bất phương trình \(2x + y \le 4\)
+ Vẽ đường thẳng d: \(2x + y = 4\) đi qua A(2;0) và B(0;4)
+ Vì \(2.0 + 0 = 0 < 4\) nên tọa độ điểm O(0;0) thỏa mãn BPT \(2x + y \le 4\)
Do đó, miền nghiệm của bất phương trình \(2x + y \le 4\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Vậy miền nghiệm của hệ bất phương trình đã cho là miền tam giác OAB (kể cả các đoạn thẳng OA, OB, AB).
c)
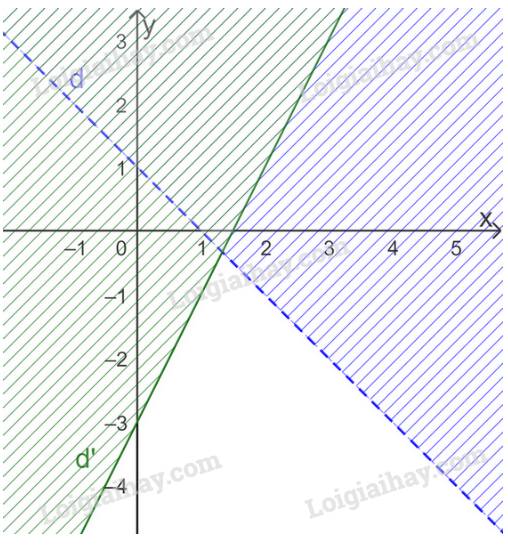
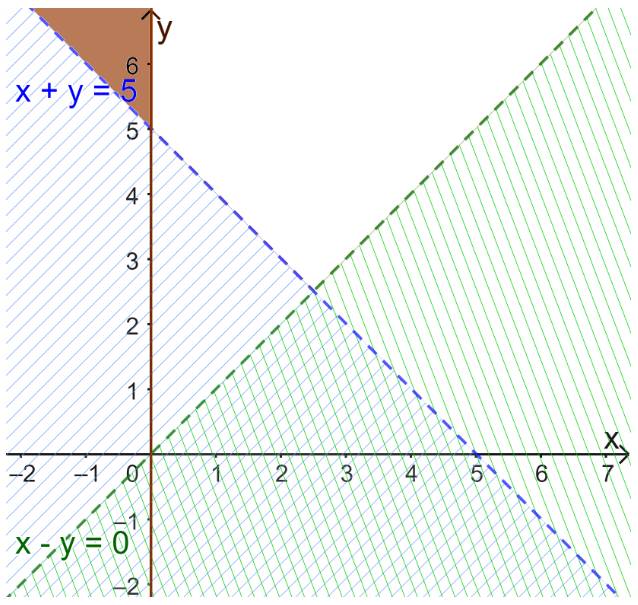
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bên phải Oy (kể cả trục Oy).
Xác định miền nghiệm của bất phương trình \(x + y > 5\)
+ Vẽ đường thẳng d: \(x + y = 5\)
+ Vì \(0 + 0 = 0 < 5\) nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình \(x + y > 5\).
Do đó, miền nghiệm của BPT \(x + y > 5\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Xác định miền nghiệm của bất phương trình \(x - y < 0\)
+ Vẽ đường thẳng d: \(x - y = 0\)
+ Vì \(1 - 0 = 1 > 0\) nên tọa độ điểm (1;0) không thỏa mãn bất phương trình \(x - y < 0\)
Do đó, miền nghiệm của bất phương trình \(x - y < 0\) là nửa mặt phẳng bờ d’ không chứa điểm (1;0).
Vậy miền nghiệm của hệ bất phương trình đã cho là miền màu trắng (không kể d và d’)

a)\(\left\{{}\begin{matrix}2m-1>0\Rightarrow m>\dfrac{1}{2}\left(1\right)\\m^2-\left(m-2\right)\left(2m-1\right)< 0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow m^2-\left(2m^2-m-4m+2\right)=-m^2+5m-2< 0\)
\(m^2-5m+2>0\Rightarrow\left[{}\begin{matrix}m< \dfrac{5-\sqrt{17}}{2}< \dfrac{1}{2}\\m>\dfrac{5+\sqrt{17}}{2}\end{matrix}\right.\)
Nghiệm hệ là
\(m>\dfrac{5+\sqrt{17}}{2}\)
b)\(\left\{{}\begin{matrix}m^2-m-2< 0\left(1\right)\\\left(2m-1\right)^2-4\left(m^2-m-2\right)\le0\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\left(2m-1\right)^2-4\left(m^2-m-2\right)=9< 0,\forall m\).
Suy ra (2) vô nghiệm .
Kết luận hệ vô nghiệm.

\(\left\{{}\begin{matrix}2x-\left(m^2+m+1\right)y=-m^2-9\left(1\right)\\m^4x+\left(2m^2+1\right)y=1\left(2\right)\end{matrix}\right.\)
rút x từ (1) thế vào (2)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\left(m^2+m+1\right)y-m^2-9}{2}\left(3\right)\\m^4\left[\dfrac{\left(m^2+m+1\right)y-m^2-9}{2}\right]+\left(2m^2+1\right)y=1\left(4\right)\end{matrix}\right.\)
\(\left(4\right)\Leftrightarrow m^4\left(m^2+m+1\right)y-m^4\left(m^2+9\right)+2\left(2m^2+1\right)y=2\)
\(\Leftrightarrow\left[m^4\left(m^2+m+1\right)+4m^2+2\right]y=m^4\left(m^2+9\right)+2\)
\(\Leftrightarrow Ay=B\)
Taco
\(\left\{{}\begin{matrix}m^2+m+1=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall m\in R\\4m^2+2>0\forall m\in R\\m^4\left(m^2+9\right)>0\forall m\in R\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A>0\forall m\in R\\B>0\forall m\in R\end{matrix}\right.\)
\(\Rightarrow y>0\forall m\in R\)
Kết luận không có m thủa mãn

Tham khảo:
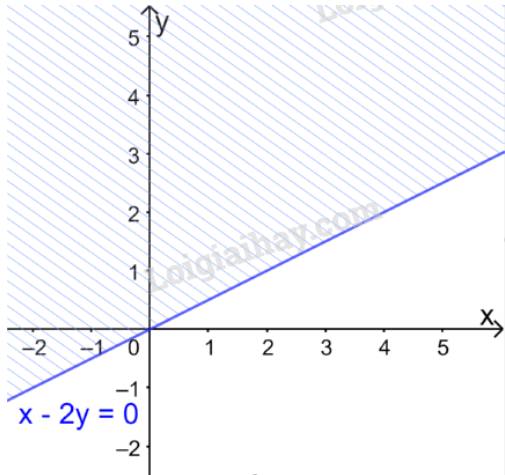
Vẽ đường thẳng \(d:x - 2y = 0\) đi qua hai điểm \(O(0;0)\) và \(B\left( {2;1} \right)\)
Xét điểm \(A(1;0).\) Ta thấy \(A \notin \Delta \) và \(1 - 2.0 = 1> 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d\), chứa điểm A
(miền không gạch chéo trên hình)
Vẽ đường thẳng \(d':x + 3y = 3\) đi qua hai điểm \(A'(0;1)\) và \(B'\left( {3;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 + 3.0 = 0 < 3\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(d'\), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
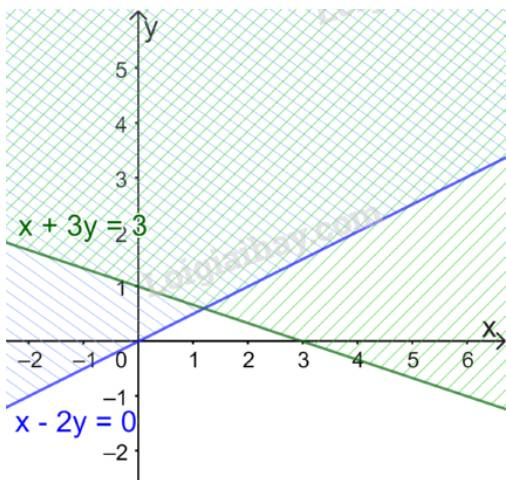
Vậy miền không gạch chéo trong hình trên là miền nghiệm của hệ bất phương trình đã cho

Tham khảo:
Xác định miền nghiệm của bất phương trình \(x + y < 1\)
+ Vẽ đường thẳng d: x+y=1 (nét đứt) đi qua (0;1) và (1;0)
+ Vì 0+0=0 < 1 nên điểm O(0;0) thuộc miền nghiệm của bpt
Do đó, miền nghiệm của bất phương trình \(x + y < 1\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Xác định miền nghiệm của bất phương trình \(2x - y \ge 3\)
+ Vẽ đường thẳng d’: \(2x - y = 3\) đi qua (1;-1) và (0;-3)
+ Vì 2.0-0=0
Do đó, miền nghiệm của bất phương trình \(2x - y \ge 3\) là nửa mặt phẳng bờ d’ không chứa gốc tọa độ O.
Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không đường thẳng d’).