Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi độ dài mỗi cạnh là x,y,z
vì x,y,z thỉ lệ thuận 2;5;9
\(\Rightarrow\)\(\frac{x}{2}=\frac{y}{5}=\frac{z}{9}\)
áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{9}=\frac{z-x}{9-2}=\frac{14}{7}=2\)
từ \(\frac{x}{2}=2\Rightarrow x=4\)
\(\frac{y}{5}=2\Rightarrow y=10\)
\(\frac{z}{9}=2\Rightarrow z=18\)
vậy x = 4; y = 10; z = 18.
Gọi độ dài 3 cạnh của tam giác đó lần lượt là a,b,c (m) (c>b>a>0)
Theo bài ra ta có:
a:b:c=2:5:9⇒a2=b5=c9a:b:c=2:5:9⇒a2=b5=c9
c−a=14c−a=14. Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a2=b5=c9=c−a9−2=147=2a2=b5=c9=c−a9−2=147=2
⇒⎧⎩⎨⎪⎪a2=2⇒a=2⋅2=4b5=2⇒b=2⋅5=10c9=2⇒c=2⋅9=18⇒{a2=2⇒a=2⋅2=4b5=2⇒b=2⋅5=10c9=2⇒c=2⋅9=18 (thỏa mãn)
Vậy độ dài 3 cạnh của tam giác đó lần lượt là 4m; 10m; 18m

Gọi độ dài 3 cạnh lần lượt là a,b,c(m)
Ta có: a,b,c tỉ lệ với 2;5;9 nên a/2=b/5=c/9
có: c-a=14
Áp dụng tính chất dãy tỉ số bằng nhau, ta được:
a/2=b/5=c/9=(c-a)/(9-2)=14/7=2
Do đó, *)a/2=2 nên a=2*2=4
*)b/5=2 nên b=2*5=10
*)c/9=2 nên c=2*9=18
Vậy độ dài 3 cạnh theo thứ tự từ bé đến lớn là: 4;10;18(m)
mk nghĩ đơn vị lớn quá, cm hoặc dm thôi

Gọi độ dài 3 cạnh của tam giác đó tỉ lệ với 2; 5;9 lần lượt là x(m); y(m); z(m). ĐK: x, y, z >0.
Theo bài ra, ta có:\(\frac{x}{2}=\frac{y}{5}=\frac{z}{9}\)và z-x= 14
Theo tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{9}=\frac{z-x}{9-2}=\frac{14}{7}=2\)\(\Rightarrow\hept{\begin{cases}x=2.2=4\left(TM\right)\\y=2.5=10\left(TM\right)\\z=2.9=18\left(TM\right)\end{cases}}\)
Vậy độ dài 3 cạnh của tam giác đó là 4m; 10m; 18m.

Gọi độ dài 3 cạnh của tam giác lần lượt là x, y, z (đơn vị: m)
Ba cạnh tỉ lệ với 3; 4; 5 => \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Cạnh lớn nhất hơn cạnh nhỏ nhất 6m => z - x = 6.
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{z-x}{5-3}=\frac{6}{2}=3\)
\(\frac{x}{3}=3\Rightarrow x=3.3=9\)
\(\frac{y}{4}=3\Rightarrow y=3.4=12\)
\(\frac{z}{5}=3\Rightarrow z=3.5=15\)
Vậy, độ dài mỗi cạnh của tam giác lần lượt là 9; 12; 15 (m)
@Nghệ Mạt
#cua

Gọi độ dài các cạnh của tam giác lần lượt là x, y, z (cm)
Theo đề bài ta có:
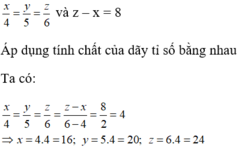
Chọn đáp án A
Gọi độ dài 3 cạnh của tam giác đó lần lượt là a,b,c (m) (c>b>a>0)
Theo bài ra ta có:
\(a:b:c=2:5:9\Rightarrow\frac{a}{2}=\frac{b}{5}=\frac{c}{9}\)
\(c-a=14\). Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{5}=\frac{c}{9}=\frac{c-a}{9-2}=\frac{14}{7}=2\)
\(\Rightarrow\begin{cases}\frac{a}{2}=2\Rightarrow a=2\cdot2=4\\\frac{b}{5}=2\Rightarrow b=2\cdot5=10\\\frac{c}{9}=2\Rightarrow c=2\cdot9=18\end{cases}\) (thỏa mãn)
Vậy độ dài 3 cạnh của tam giác đó lần lượt là 4m; 10m; 18m
gọi độ dài 3 cạnh của 1 tam giác là a, b,c (a,b,c>0, m)
+vì độ dài 3 cạnh tỉ lệ với 2;5;9
\(\Rightarrow\) \(\frac{a}{2}\) = \(\frac{b}{5}\) = \(\frac{c}{9}\)
+ vì canh nhỏ nhất ngắn hơn cạnh lớn nhất là 14m
\(\Rightarrow\) c-a= 14
áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{c-a}{9-2}\)= \(\frac{14}{7}\)= 2
\(\Rightarrow\) a= 2.2= 4
b= 5.2= 10
c= 9.2= 18
vậy độ dài 3 cạnh của 1 tam giác lần lượt là: 4m; 10m; 18m