
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

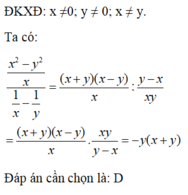



\(P=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)-4x^2=\left(x-y-x-y\right)^2-\left(2x\right)^2=\left(-2y\right)^2-\left(2x\right)^2\)
\(=\left(2y-2x\right)\left(2y+2x\right)=2\left(y-x\right)2\left(y+x\right)=4\left(x+y\right)\left(y-x\right)\)
\(x^3-x^2y+3x-3y=x^2\left(x-y\right)+3\left(x-y\right)=\left(x-y\right)\left(x^2+3\right)\)
\(x^3-2x^2-4xy^2+x=x\left(x^2-2x+1-4y^2\right)=x\left[\left(x-1\right)^2-\left(2y\right)^2\right]=x\left(x+2y-1\right)\left(x-2y-1\right)\)
\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-8=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-8\)
Đặt \(x^2+7x+10=t\), ta có:
\(t\left(t+2\right)-8=t^2+2t-8=t^2-2t+4t-8=t\left(t-2\right)+4\left(t-2\right)=\left(t-2\right)\left(t+4\right)\)
\(=\left(x^2+7x+10+4\right)\left(x^2+7x+10-2\right)=\left(x^2+7x+14\right)\left(x^2+7x-8\right)\)

Lời giải:
\(B=x(x^2+xy+y^2)-y(y^2+xy+y^2)\)
\(=(x-y)(x^2+xy+y^2)=x^3-y^3=10^3-(-1)^3=1000-(-1)=1001\)
\(C=x^4+10x^3+10x^2+10\)
\(=x^4+9x^3+x^3+9x^2+x^2+10\)
\(=x^3(x+9)+x^2(x+9)+x^2+10\)
\(=(x+9)(x^3+x^2)+x^2+10\)
\(=(-9+9)[(-9)^3+(-9)^2]+(-9)^2+10\)
\(=0+(-9)^2+10=91\)
Thay $x=-1$ vào biểu thức:
\(D=x^2(x+y)-xy(x-y)-x(y^2+1)\)
\(=(-1)^2(x+y)-(-1)y(x-y)-(-1)(y^2+1)\)
\(=x+y+y(x-y)+(y^2+1)\)
\(=x+y+xy-y^2+y^2+1=x+y+xy+1\)
\(=(x+1)(y+1)=(-1+1)(y+1)=0\)

Bài 2:
a, x( x-y)+ y(x+y) tại x=-6 và y=8
= x\(^2\) + xy + xy - y\(^2\)
= x\(^2\) + 2xy - y\(^2\)
Thay x = 8 và y = 7
Ta có: (-8)\(^2\) + 2. (-8).7 - 7 \(^2\)
= -97
b, x(x22- y)- x22(x +y) +y( x22- x) tại x=\(\dfrac{1}{2}\)và y =-100
= x\(^3\) - xy + xy\(^2\) - xy - x\(^3\) - xy\(^2\)
= -2xy
Thay x = \(\dfrac{1}{2}\)và y =-100
Ta có: -2.\(\dfrac{1}{2}\) .(-100)
= 100
Bài 1,
a, 3x(12x-4)-9x(4x-3x)=30
\(\Leftrightarrow\)\(36x^2-12x-36x^2+27x^2=30\)
\(\Rightarrow15x=30\)
\(\Rightarrow x=2\)
Bài 2,
a, x(x-y)+y(x+y)
\(\Leftrightarrow x^2-xy+xy+y^2\)
\(\Rightarrow\)\(x^2+y^2\)
Tại x=-6 và y=8,ta có;
\(x^2+y^2=\left(-6\right)^2+8^2=36+64=100\)
b, x(\(x^2-y)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(\Leftrightarrow x^3-xy-x^3-x^2y+x^2y-xy\)
\(\Rightarrow-2xy\)
Tại x=à y =(-100),Ta có
-2xy=-2.\(\dfrac{1}{2}\).-100=100
Bài 3:
a.x(x-y)+y(x-y)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)\)
\(\Rightarrow\)\(x^2-y^2\)

\(A=\left(x+y\right)^2-2xy=25-12=13\)
\(B=\left(x+y\right)\left(x^2+y^2-xy\right)=\left(x+y\right)\left[\left(x+y\right)^2-3xy\right]=5\left(25-18\right)=35\)
\(C=x^2-y^2\Rightarrow C^2=x^4+y^4-2x^2y^2=\left(x^2+y^2\right)^2-4x^2y^2\)
\(C^2=\left[\left(x+y\right)^2-2xy\right]^2-4\left(xy\right)^2=\left(25-12\right)^2-4.36=25\Rightarrow C=\pm5\)
\(D=\frac{x^2+y^2}{xy}=\frac{\left(x+y\right)^2-2xy}{xy}=\frac{25-12}{6}=\frac{13}{6}\)