Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

dễ mà bạn những câu này trong sách giáo khoa chỉ rõ mà, bạn phải cố gắng suy nghĩ đi không hiểu có thể hỏi thầy cô nhé !!

BT1.
Ta có: \(2009^{20}=2009^{10}\times2009^2\)và \(20092009^{10}=2009^{10}\times10001^{10}\)
Rõ ràng \(2009^2< 10001^{10}\\ \Rightarrow2009^{10}\times2009^2< 2009^{10}\times10001^{10}\\ \Rightarrow2009^{20}< 20092009^{10}\left(đpcm\right)\)
BT9. Bn xem lại đề bài đi. \(x^2+x+1\) luôn lớn hơn 0 mà bn.
BT3.
Giả sử \(M\in N\)
Nên:
\(\left\{{}\begin{matrix}\dfrac{x}{x+y+z}\in N\\\dfrac{y}{y+x+t}\in N\\\dfrac{z}{z+t+y}\in N\\\dfrac{t}{t+z+x}\in N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮x+y+z\\y⋮y+x+t\\z⋮z+t+y\\t⋮t+z+x\end{matrix}\right.\)
Vì \(x,y,z,t\in N\)*\(\Rightarrow x,y,z,t>0\)\(\Rightarrow\left\{{}\begin{matrix}x>x+y+z\\y>x+y+t\\z>y+z+t\\t>x+z+t\end{matrix}\right.\)(vô lí)
Vậy rõ ràng điều giả sử là vô lí. Nên \(M\notin N\left(đpcm\right)\)
Mình chỉ giúp đc đến đây thôi, mong bn thông cảm
Ngoài ra, chúc bn học tốt nhé![]()
![]()
![]()
![]()
![]()
Bài toán 2.
Ta có: \(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+....+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\dfrac{2009-1}{1}+\dfrac{2009-2}{2}+\dfrac{2009-3}{3}+...+\dfrac{2009-2008}{2008}\)
\(=2009-1+\dfrac{2009}{2}-1+\dfrac{2009}{3}-1+....+\dfrac{2009}{2008}-1\)
\(=2009+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{....1}{2008}\right)-1.2008\)
\(=\left(2009-2008\right)+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=1+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
=\(2009.A\)
Do đó, tỉ số \(\dfrac{A}{B}=\dfrac{A}{2009.A}=\dfrac{1}{2009}\)

a) Dấu hiệu: Thời gian giải một bài toán
Số giá trị khác nhau: 8
b) Bảng "tần số"
![]()
Nhận xét
Thời gian giải 1 bài toán của 35 học sinh chỉ nhận 8 giá trị khác nhau, người giải nhanh nhất là 3 phút (có 1 học sinh), người giải chậm nhất là 10 phút, thời gian giải xong chủ yếu từ 6 đến 8 phút.
a, dấu hiệu ở đây là: thời gian giải một bài toán
-
số các giá trị là: 35
bảng tần số là:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Ta biết rằng 1 giờ = 60 phút = 3600 giây.
Do đó khi kim giờ đi được 1 giờ thì kim phút đi đwọc 1 vòng và kim giây quay đwọc 60 vòng trên mặt đồng hồ.
Vậy trên mặt chiếc đồng hồ khi kim giờ quay được 1 vòng thì kim phút quay được 1.12 = 12 (vòng) và kim giây quay được 60.12 = 720 (vòng)
Ta biết rằng 1 giờ = 60 phút = 3600 giây.
Do đó khi kim giờ đi được 1 giờ thì kim phút đi đwọc 1 vòng và kim giây quay đwọc 60 vòng trên mặt đồng hồ.
Vậy trên mặt chiếc đồng hồ khi kim giờ quay được 1 vòng thì kim phút quay được 1.12 = 12 (vòng) và kim giây quay được 60.12 = 720 (vòng)
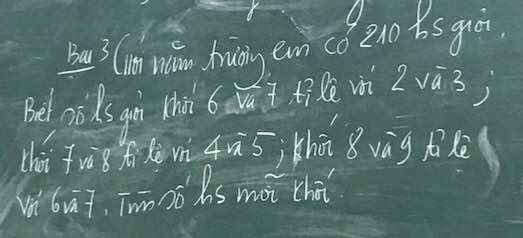
















Gọi số học sinh khối 6;7;8;9 lần lượt là a,b,c,d
Ta có: a:b=2:3
nên \(\dfrac{a}{2}=\dfrac{b}{3}\)
hay \(\dfrac{a}{8}=\dfrac{b}{12}\left(1\right)\)
Ta có: b:c=4:5
nên \(\dfrac{b}{4}=\dfrac{c}{5}\)
hay \(\dfrac{b}{12}=\dfrac{c}{15}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\dfrac{a}{8}=\dfrac{b}{12}=\dfrac{c}{15}\)
hay \(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}\left(3\right)\)
Ta có: c:d=6:7
nên \(\dfrac{c}{6}=\dfrac{d}{7}\)
hay \(\dfrac{c}{30}=\dfrac{d}{35}\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}\)
mà a+b+c+d=210
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{16}=\dfrac{b}{24}=\dfrac{c}{30}=\dfrac{d}{35}=\dfrac{a+b+c+d}{16+24+30+35}=\dfrac{210}{105}=2\)
Do đó: a=32; b=48; c=60; d=70