Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi tử số là x
Mẫu số sẽ là : x + 11 ( x khác -11)
Ta có phân số đó là: \(\frac{x}{x+11}\)
Bớt tử số 7 đơn vị và tăng mẫu số lên 4 đơn vị ta có: \(\frac{x-7}{x+15}\)( x khác -15)
Theo bài ra ta có phương trình: \(\frac{x-7}{x+15}=\frac{x+11}{x}\)( x khác 0; -11; -15)
<=> \(x\left(x-7\right)=\left(x+11\right)\left(x+15\right)\)
<=> \(x^2-7x=x^2+26x+165\)
<=> \(x=-5\)
Vậy phân số đó là: \(\frac{-5}{6}\)

5/10 bn nhé
~~~~~~~~~~~~~~
li-ke cho mìh nhé bn Lưu Thị Hoàn

17. Nửa chu vi miếng đất là: \(48:2=24\left(m\right)\)
Gọi chiều rộng, chiều dài miếng đất ban đầu lần lượt là a (m) và b (m) \(\left(0< a;b< 24\right)\)
Theo bài ra, ta có:
\(\hept{\begin{cases}a+b=24\\\left(a-2\right)\left(b+6\right)-ab=12\end{cases}}\Leftrightarrow\hept{\begin{cases}a+b=24\\6a-2b=24\end{cases}}\Leftrightarrow\hept{\begin{cases}a=9\\b=15\end{cases}}\)(thỏa mãn)
Diện tích miếng đất ban đầu là: \(a.b=9.15=135\left(m^2\right)\)

Câu hỏi của tran gia nhat tien - Toán lớp 8 - Học toán với OnlineMath tham khảo nha
Học tốt

Gọi tử số của phân số ban đầu là x
thì mẫu số của phân số ban đầu là: x + 12
Vậy phân số ban đầu là: \(\frac{x}{x+12}\)
Theo bài ra ta có:
\(\frac{x-3}{x+12-3}=\frac{1}{4}\)
\(\Leftrightarrow\)\(\frac{x-3}{x+9}=\frac{1}{4}\)
\(\Leftrightarrow\)\(4\left(x-3\right)=x+9\)
\(\Leftrightarrow\)\(4x-12=x+9\)
\(\Leftrightarrow\)\(3x=21\)
\(\Leftrightarrow\)\(x=7\)
Mẫu số là: 7 + 12 = 19
Vậy phân số ban đầu là: 7/19

Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
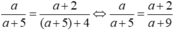
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10