Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)
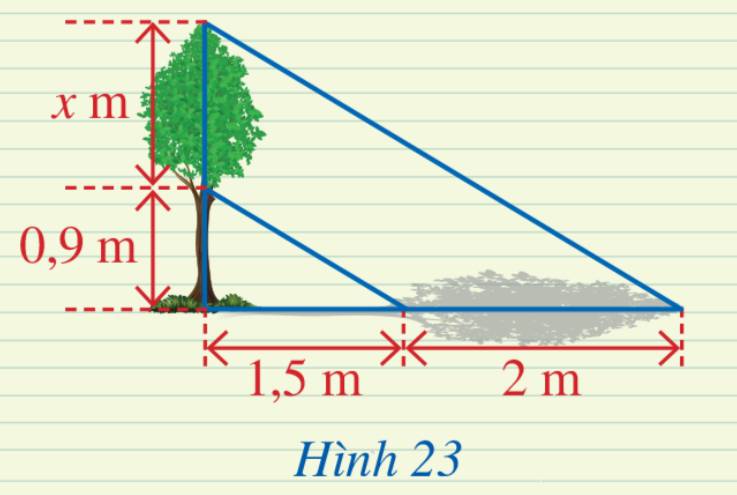
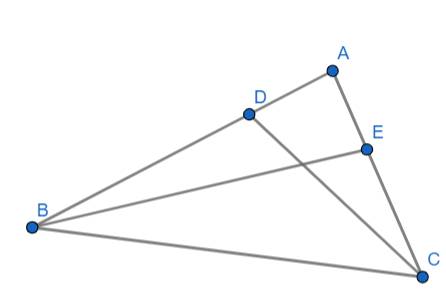
Đoạn thẳng AB biểu thị cho độ cao của cây, đoạn thẳng AD và DB biểu thị độ cao của thân và tán cây, đoạn thẳng AE và EC biểu thị độ dài cái bóng của thân cây và tán cây, đoạn thẳng DE và BC biểu thị cho các tia nắng.
Xét tam giác ABC với \(DE\parallel BC\) ta có:
\(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\) (Định lý Thales)
\(\begin{array}{l} \Rightarrow \frac{{0,9}}{x} = \frac{{1,5}}{2}\\ \Rightarrow 0,9.2 = 1,5x\\ \Rightarrow 1,8 = 1,5x\\ \Rightarrow x = 1,2\end{array}\)
Vậy độ cao \(x\) là 1,2 m.
Vì tổng ba góc trong một tam giác bằng \(180^\circ \) nên nếu \(\widehat {PMN} = \widehat {ACB},\,\,\widehat {PNM} = \widehat {BAC}\) thì \(\widehat {MPN} = \widehat {CBA}\)
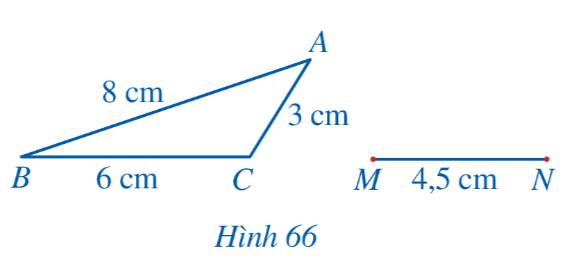
Ta cần \(\Delta ABC \backsim\Delta NPM\)
Khi đó \(\frac{{AB}}{{NP}} = \frac{{BC}}{{PM}} = \frac{{AC}}{{NM}}\) hay \(\frac{8}{{NP}} = \frac{6}{{PM}} = \frac{3}{{4,5}} = \frac{2}{3}\)
Ta có: \(\frac{8}{{NP}} = \frac{2}{3} \Rightarrow NP = 8.3:2 = 12cm\)
\(\frac{6}{{MP}} = \frac{2}{3} \Rightarrow MP = 6.3:2 = 9cm\)
Vậy Thanh cần dùng thước kẻ vẽ hai đoạn thẳng NP=12cm và PM=9cm để tìm được điểm P thỏa mãn yêu cầu đề bài.
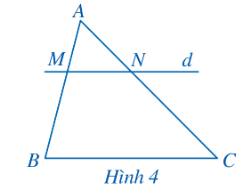
Xét tam giác ABC với \(MN\parallel BC\), ta có \(\frac{{MB}}{{AB}} = \frac{{NC}}{{AC}}\) (định lý Thales).
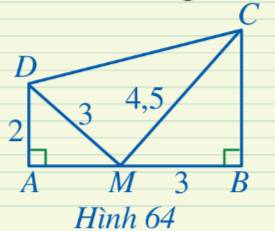
Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\) nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có \(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).
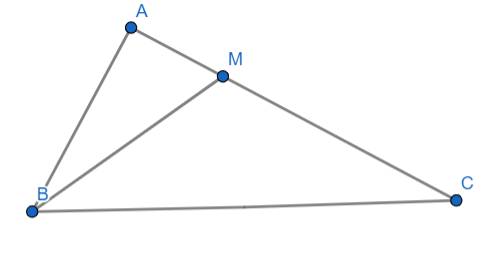
a) Áp dụng định lý Py-ta-go cho tam giác ABC vuông tại A ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{10^2+20^2}=10\sqrt{5}\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác ABM vuông tại A ta có:
\(BM^2=AB^2+AM^2\)
\(\Rightarrow BM=\sqrt{AB^2+AM^2}\)
\(\Rightarrow BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b) Ta có:
\(\dfrac{AM}{AB}=\dfrac{1}{2}\)
\(\dfrac{BM}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
Xét hai tam giác ABC và AMB có:
\(\widehat{BAC}\) chung
\(\dfrac{AM}{AB}=\dfrac{MB}{BC}=\dfrac{1}{2}\)
\(\Rightarrow\Delta ABC\sim\Delta AMB\left(c.g.c\right)\)
a) Xét hai tam giác ABE và ACD có:
\(\widehat{ACD}=\widehat{ABE}\left(gt\right)\)
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACD\left(g.g\right)\)
b) Ta có: \(\Delta ABE\sim\Delta ACD\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AE}{AD}\)
a) 
b) Phương trình hoành độ giao điểm của hai đường thẳng là:
\(x-1=2x\)
\(\Leftrightarrow2x-x=-1\)
\(\Leftrightarrow x=-1\)
Thay x = - 1 vào y = 2x ta có: \(y=2\cdot-1=-2\)
Vậy tọa độ giao điểm của 2 đường thẳng là \(\left(-1;-2\right)\)
Đoạn thẳng AB biểu diễn cho cái que.
Trên bàn cờ lấy một điểm P nằm ngoài đoạn thẳng AB sao cho AP có độ dài 6 ô vuông.
Nối AP, BP.
Trên đoạn thẳng AP lấy hai điểm M và N sao cho AM = MN = NP = 2 ô vuông.
Tại M, N kẻ các đường thẳng vuông góc với AP và cắt AB lần lượt tại C và D.
=> MC // NO // PB
Áp dụng định lý Thales trong tam giác APB thì \(\frac{AM}{AP} = \frac{AC}{AB} = \frac{1}{3} \Rightarrow AC = \frac{1}{3}AB\) và \(\frac{AN}{AP} = \frac{AD}{AB} = \frac{2}{3}\Rightarrow AD = \frac{2}{3}AB\).
Khi đó AC = CD = DB = \(\frac{1}{3}\)AB.
Vậy ta đã chia cái que thành 3 phần bằng nhau mà không cần dùng thước đo.