Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

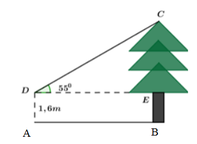
Đặt các điểm D, E như hình vẽ.
Xét CDE vuông tại E ta có:
![]()
Chiều cao của cây là BC = CE + BE = 8,57 + 1,6 = 10,17m
Đáp án cần chọn là: D

Với góc nhìn tạo với phương nằm ngang là 42 độ, ta có:
tan(42°) = h / 15
Để tìm giá trị của h, ta cần giải phương trình trên để tìm giá trị của h.
tan(42°) = h / 15
h = tan(42°) * 15
Sử dụng máy tính, ta tính được:
h ≈ 15.7m
Vậy, chiều cao của cây là khoảng 15.7m.

*gọi: A là đỉnh ngọn đèn biển; B là chân đèn; C là hòn đảo
>>tam giác ABC vuông tại B có: AB=38m; góc ACB=30 độ
>>khoảng cách từ đảo đến chân đèn:
AC=AB/tan30=38/tan30=38căn3=65,8179m

7: ΔABC vuông tại A có AB=12m; góc B=52 độ. Tính AC
AC=AB*tan52=12*tan52=15,36(m)
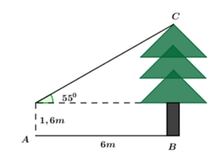
Gọi các điểm A, B, C, D, E như trên hình.
CA=\(\dfrac{AB}{tan37^o}\)=\(\dfrac{10}{tan37^o}\), CD=\(\dfrac{DE}{tan37^o}\)=\(\dfrac{1,6}{tan37^o}\), suy ra khoảng cách cần tìm là AD=CA-CD=\(\dfrac{10}{tan37^o}\)-\(\dfrac{1,6}{tan37^o}\)=\(\dfrac{8,4}{tan37^o}\)\(\approx\)11,15 (m).