Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải của bạn Hòa như trên là sai. Vì bạn đã chia cả hai vế của phương trinh cho x mà chưa biết là x = 0 hay \(x\ne0\)
Nếu \(x\ne0\)thì lời giải như trên là chính xác.
Nếu x = 0 thì phương trình có một nghiệm là 0.
Nguyễn Việt Hoàng
Bạn Hòa giải sai. Vì không thể chia hai vế của phương trình đã cho với x (bởi vì x có thể = 0) để được phương trình x + 2 = x + 3. Làm như thế này có thể làm mất nghiệm của phương trình ban đầu.
- Lời giải đúng:
(Hoặc: x(x + 2) = x(x + 3)
⇔ x(x + 2) - x(x + 3) = 0 (chuyển vế)
⇔ x(x + 2 - x - 3) = 0 (rút nhân tử chung x)
⇔ x.(-1) = 0
⇔ x = 0)

- Bạn Hòa giải sai.
Lỗi sai: Ở bước thứ hai, không thể chia hai vế của phương trình cho x vì ta chưa biết x có khác 0 hay không.
- Sửa lại:
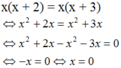
Vậy nghiệm của phương trình là x = 0

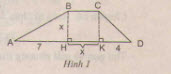
Hướng dẫn giải:
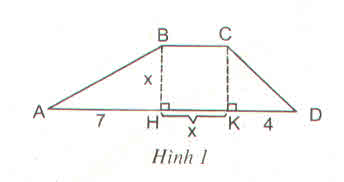
Gọi S là diện tích hình thang ABCD.
1) Theo công thức
S = BH(BC+DA)2BH(BC+DA)2
Ta có: AD = AH + HK + KD
=> AD = 7 + x + 4 = 11 + x
Do đó: S = x(11+2x)2x(11+2x)2
2) Ta có: S = SABH + SBCKH + SCKD.
= 1212.AH.BH + BH.HK + 1212CK.KD
= 1212.7x + x.x + 1212x.4
= 7272x + x2 + 2x
Vậy S = 20 ta có hai phương trình:
x(11+2x)2x(11+2x)2 = 20 (1)
7272x + x2 + 2x = 20 (2)
Cả hai phương trình không có phương trình nào là phương trình bậc nhất.
a) theo cách tính thứ nhất, diện tích hình thang là :
SABCD= BH.(BC+AD):2= x(x+7+x+4):2
=x(2x+11):2 = \(\dfrac{1}{2}\)x(2x+11) (đvdt) (1)
b) theo cách tính thứ hai
SABCD=SAHB+SCKD= \(\dfrac{1}{2}\).7x+x2+\(\dfrac{1}{2}\).4x
=\(\dfrac{7x+2x^2+4x}{2}\)= \(\dfrac{2x^2+11x}{2}\) (đvdt) (2)
Với S = 20 thì (1) và (2) trở thành x2+5,5x =20 thì đây là một phương trình bậc hai (vì có x2).
Vậy trong hai phương trình trên không có phương trình nào là phương trình bậc nhất.

a) 3x+2(x-5)=-x+2
<=> 3x+2x+x=2+10
<=>6x=12
<=>x=2
b) 3x2-2x=0
<=>x(3x-2)=0
<=>\(\left[{}\begin{matrix}x=0\\3x-2=0\end{matrix}\right.\)
<=>\(\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
c) \(\dfrac{2x}{3}\)+\(\dfrac{x-4}{6}\)=2-\(\dfrac{x}{2}\)
<=>\(\dfrac{8x+2x-8}{12}\)=\(\dfrac{24-6x}{12}\)
<=> 8x+2x-8=24-6x
<=>8x+2x+6x=24+8
<=>16x=32
<=>x=2
d) \(\dfrac{x-2}{x+2}\)-\(\dfrac{3}{x-2}\)= -\(\dfrac{2\left(x-11\right)}{4-x^2}\) ( ĐKXĐ: x\(\ne\)\(\pm\)2)
<=> \(\dfrac{\left(x-2\right)^2-3\left(x+2\right)}{x^2-4}\)=\(\dfrac{2\left(x-11\right)}{x^2-4}\)
=> (x-2)2-3(x+2)=2(x-11)
<=> x2-4x+4-3x-6=2x-22
<=> x2-4x-3x-2x=-22-4+6
<=> x-9x+20=0
<=> (x-4)(x-5)=0
<=>\(\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\) ( thỏa mãn diều kiện )
d) (x2+1)(x2-4x+4)=0
=> x2-4x+4=0 (x2+1\(\ge\)1 với mọi x)
=>(x-2)2 =0
=>x=2

Bài 1:
a) \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}>\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
{bước 1 là quy đồng bỏ mẫu, bạn chọn mẫu là BCNN của các mẫu số ở tất cả các phân thức trong BPT, phải chọn MC là BCNN vì số càng đơn giản càng dễ tính toán}
\(\Leftrightarrow2x-3+5x^2-10x>5x^2-14x+21\)
{chuyển vế}
\(\Leftrightarrow2x-10x+14x>21+3\) \(\Leftrightarrow6x>24\)
{chia cả 2 vế của bpt cho 6}
\(\Leftrightarrow x>4\)
Vậy nghiệm của BẤT phương trình là x>4
{bạn chú ý là bất phương trình chứ KHÔNG PHẢI là nghiệm của phương trình nhé}
cũng có thể kết luận thế này: Vậy S={x|x>4}
hay biểu diễn trên trục số (nếu đề yêu cầu)
{khi đã biểu diễn trên trục số thì bạn không cần phải kết luận như 2 cách trên nữa nhé, dư đấy.}
1b)
\(\dfrac{6x+1}{18}+\dfrac{x+3}{12}\le\dfrac{5x+3}{6}+\dfrac{12-5x}{9}\)
{tương tự: quy đồng bỏ mẫu}
\(\Leftrightarrow12x+2+3x+9\le30x+18+48-20x\)
{chuyển vế các hạng tử}
\(\Leftrightarrow15x-10x\le66-11\)\(\Leftrightarrow5x\le55\)
{chia cả 2 vế cho 5}
\(\Leftrightarrow x\le11\)
Vậy \(x\le11\)
(cách kết luận như câu a, nói rồi không nói lại nhé ^^!)

\(a,\left(x+1\right)^2-\left(x-1\right)^2-3\left(x+1\right)\left(x-1\right)\)
\(=x^2+2x+1-\left(x^2-2x+1\right)-3\left(x^2-1\right)\)
\(=x^2+2x+1-x^2+2x-1-3x^2+2=-3x^2+4x+2\)\(b,5\left(x+2\right)\left(x-2\right)-\left(2x-3\right)^2-x^2+17\)
\(=5\left(x^2-4\right)-\left(4x^2-12x+9\right)-x^2+17\)
\(=5x^2-20-4x^2+12x-9-x^2+17=12x-12\)

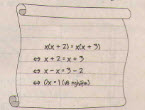
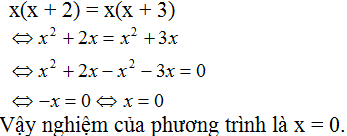



- Bạn Hòa giải sai. Vì không thể chia hai vế của phương trình đã cho với x (bởi vì x có thể = 0) để được phương trình x + 2 = x + 3. Làm như thế này có thể làm mất nghiệm của phương trình ban đầu.
- Lời giải đúng:
(Hoặc: x(x + 2) = x(x + 3)
\(\Leftrightarrow\) x(x + 2) - x(x + 3) = 0 (chuyển vế)
\(\Leftrightarrow\) x(x + 2 - x - 3) = 0 (rút nhân tử chung x)
\(\Leftrightarrow\) x.(-1) = 0
\(\Leftrightarrow\) x = 0)