Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
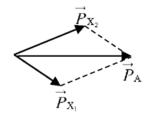
Khi cho hạt nhân A (đạn) bắn vào hạt nhân B (bia) sinh ra hai hạt X giống nhau có cùng vận tốc và hai hạt X hợp với nhau một góc α thì A + B → X 1 + X 2
Do hai hạt sinh ra giống nhau có cùng động năng nên
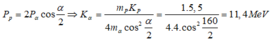
Kết hợp ĐLBT và chuyển hóa năng lượng
![]()
Chú ý: (với p 2 = 2 K m )
Chứng minh: Xuất phát ĐLBT động lượng P A = P X 1 + P X 2
Vì cùng vận tốc và giống nhau nên khối lượng sẽ giống nhau suy ra hai hạt X có cùng động năng kéo theo đó cùng độ lớn vecto động lượng.
Bình phương vô hướng ta được P 2 A = 2 P 2 X cos α
1 + cos α = 2 cos 2 α 2
P 2 A = 4 P 2 X cos 2 α 2 ⇒ P A = P X cos α 2
*Kết hợp với ĐLBT và chuyển hóa NL ta có hệ 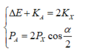

\(_2^4 He + _{13}^{27}Al \rightarrow _{15}^{30}P + _0^1n\)
Phản ứng thu năng lượng
\( K_{He} - (K_{P}+K_{n} )= 2,7MeV.(*)\)
Lại có \(\overrightarrow v_P = \overrightarrow v_n .(1)\)
=> \(v_P = v_n\)
=> \(\frac{K_P}{K_n} = 30 .(2)\)
Áp dụng định luật bảo toàn động lượng trước và sau phản ứng
\(\overrightarrow P_{He} = \overrightarrow P_{P} + \overrightarrow P_{n} \)
Do \(\overrightarrow P_{P} \uparrow \uparrow \overrightarrow P_{n}\)
=> \(P_{He} = P_{P} + P_{n} \)
=> \(m_{He}.v_{He} = (m_{P}+ m_n)v_P=31m_nv\) (do \(v_P = v_n = v\))
=> \(K_{He} = \frac{31^2}{4}K_n.(3)\)
Thay (2) và (3) vào (*) ta có
\(K_{He}-31K_n= 2,7.\)
=> \(K_{He} = \frac{2,7}{1-4/31} = 3,1MeV.\)

Đáp án C
Khi cho hạt nhân A ( đạn) bắn vào hạt nhân B (bia) sinh ra hai hạt X giống nhau có cùng vận tốc và hai hạt X hợp với nhau một góc α thì A + B → X 1 + X 2
v Do hai hạt sinh ra giống nhau có cùng động năng nên
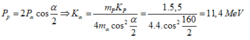
Kết hợp ĐLBT và chuyển hóa năng lượng
![]()
Chú ý: (Với p 2 = 2 K m )
Chứng minh: Xuất phát ĐLBT động lượng P A = P X 1 + P X 2
Vì cùng vận tốc và giống nhau nên khối lượng sẽ giống nhau suy ra hai hạt X có cùng động năng kéo theo đó cùng vecto động lượng.
Bình phương vô hướng ta được
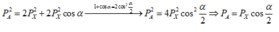
*Kết hợp với ĐLBT và chuyển hóa NL ta có hệ 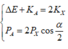

\(_1^1p + _4^9Be \rightarrow \alpha + _3^6Li\)
Phản ứng này thu năng lượng => \(W_{thu} =(m_s-m_t)c^2 = K_t-K_s\)
=> \( K_p+ K_{Be}-K_{He}- K_{Li} = W_{thu} \) (do Be đứng yên nên KBe = 0)
=> \(K_p = W_{thu}+K_{Li}+K_{He} = 2,125+4+3,575 = 9,7MeV.\)
Áp dụng định luật bảo toàn động lượng
P P P α α p Li
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có
Áp dụng định lí hàm cos trong tam giác
=> \(\cos {\alpha} = \frac{P_p^2+P_{He}^2-P_{Li}^2}{2P_pP_{He}} = \frac{2.1.K_p+ 2.4.K_{He}-2.6.K_{Li}}{2.2.2m_pm_{He}K_pK_{He}} = 0.\)
Với \(P^2 = 2mK, m=A.\).
=> \(\alpha = 90^0.\)

\(\alpha + _7^{14}N \rightarrow _1^1p + _8^{17}O\)
\(m_t-m_s = m_{\alpha}+m_N - (m_{O}+m_p) =- 1,3.10^{-3}u < 0\), phản ứng thu năng lượng.
\(W_{thu} = (m_s-m_t)c^2 = K_t-K_s\)
=> \(1,3.10^{-3}.931,5 = K_{He}+K_N- (K_p+K_O)\)(do Nito đứng yên nên KN = 0)
=> \(K_p +K_O = 6,48905MeV. (1)\)
Áp dụng định luật bảo toàn động lượng
P P α P p O
\(\overrightarrow P_{\alpha} =\overrightarrow P_{p} + \overrightarrow P_{O} \)
Dựa vào hình vẽ ta có (định lí Pi-ta-go)
\(P_{O}^2 = P_{\alpha}^2+P_p^2\)
=> \(2m_{O}K_{O} = 2m_{He}K_{He}+ 2m_pK_p.(2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_p = 4,414MeV; K_O = 2,075 MeV.\)
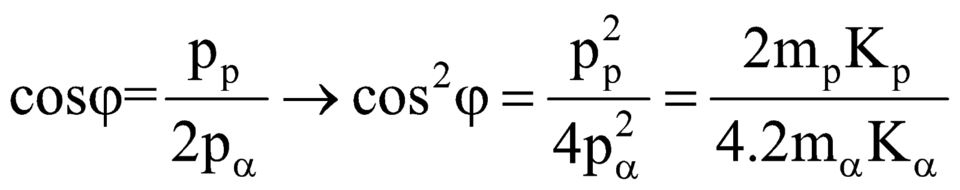
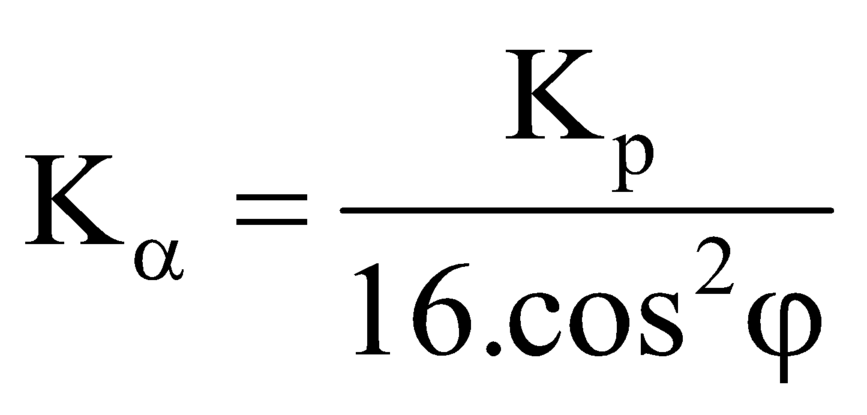

 MeV
MeV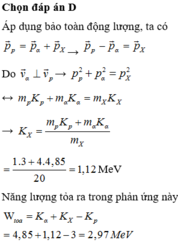
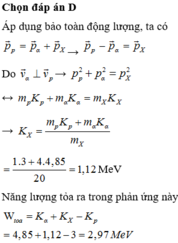
Phương pháp:
Sử dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng hạt nhân
Sử dụng định luật bảo toàn động lượng; định lí hàm số cos trong tam giác
Năng lượng toả ra của phản ứng Q = Ks – Kt (Kt và Ks lần lượt là tổng động năng của các hạt trước và sau phản ứng hạt nhân.
Cách giải:
Phương trình phản ứng hạt nhân: p 1 1 + Li 3 7 → 2 He 2 4
Năng lượng toả ra của phản ứng: Q = 2Kα – Kp
Kp = 5,5 MeV
Định luật bảo toàn động lượng: p p → = p α 1 → + p α 2 →
Áp dụng định lí hàm số cos ta có:
Þ Năng lượng toả ra của phản ứng: Q = 17,3 (MeV)
Đáp án C