Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lý Pythagoras, ta có công thức: c^2 = a^2 + b^2, trong đó c là cạnh huyền (BC), a và b là hai cạnh góc vuông (MB và MC).
Với MB = 2m và cây sào cao 6m, ta có MC = 6m - 2m = 4m.
Áp dụng công thức Pythagoras, ta có: BC^2 = MB^2 + MC^2 = 2^2 + 4^2 = 4 + 16 = 20.
Do đó, khoảng cách BC là căn bậc hai của 20: BC = √20 ≈ 4.47m (làm tròn đến hai chữ số thập phân).

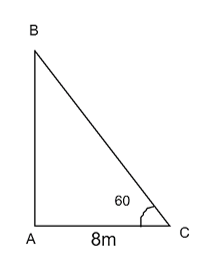
tanˆBCA=ABAC=AB8⇒tan600=AB8⇒AB=8√3(m)≈13,86mtan���^=����=��8⇒tan600=��8⇒��=83(�)≈13,86�
Vậy cây cổ thụ có chiều cao khoảng 13,86 m.

Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m