K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
18 tháng 11 2017
Chọn C
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3

CM
17 tháng 7 2018
Chọn A.
Gọi I(t;-1;-t) ∈ Δ là tâm mặt cầu (S) cần tìm.
Theo giả thiết mặt cầu tiếp xúc với hai mặt phẳng (P) và (Q) nên:
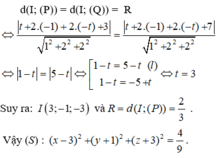

CM
1 tháng 3 2018
Đáp án D
Phương trình tham số của đường thẳng d là : d: x = 1 +2 t, y = 3+ 4t, z = t
Ta có I ∈ d => I(1 + 2t, 3 + 4t, t). Vì (S) tiếp xúc với mặt phẳng (P) nên ta có:
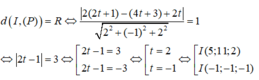


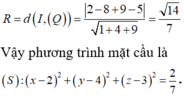
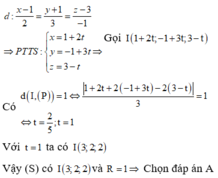
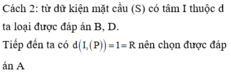
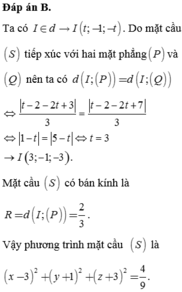

a.
\(\overrightarrow{AI}=\left(2;4;0\right)\Rightarrow R^2=AI^2=20\)
Phương trình (S):
\(\left(x-5\right)^2+\left(y-5\right)^2+z^2=20\)
b.
\(R=d\left(O;\left(\alpha\right)\right)=\dfrac{\left|16.0-15.0-12.0+75\right|}{\sqrt{16^2+15^2+12^2}}=3\)
Phương trình (S): \(x^2+y^2+z^2=9\)
c.
Đường thẳng \(\Delta\) qua \(A\left(-1;1;0\right)\) và nhận \(\overrightarrow{u}=\left(-1;1;-3\right)\) là 1 vtcp
\(\overrightarrow{AI}=\left(0;1;0\right)\)
\(R=d\left(I;\Delta\right)=\dfrac{\left|\left[\overrightarrow{AI};\overrightarrow{u}\right]\right|}{\left|\overrightarrow{u}\right|}=\dfrac{\sqrt{10}}{\sqrt{11}}\)
Phương trình (S): \(\left(x+1\right)^2+\left(y-2\right)^2+z^2=\dfrac{10}{11}\)