
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


84. Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.
a) Tứ giác AEDF là hình gi ? Vì sao ?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi ?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì ? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông ?
Bài giải:
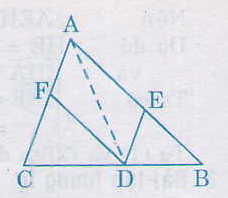
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

a)\(\frac{3xy}{9y}=\frac{\left(3y\right)x}{3.\left(3y\right)}=\frac{x}{3}\)(đúng)
b)\(\frac{3xy+3}{9y+3}=\frac{3\left(xy+1\right)}{3\left(3y+1\right)}=\frac{xy+1}{3y+1}\ne\frac{x}{3}\)(sai)
c)\(\frac{3xy+3}{9y+9}=\frac{3\left(xy+1\right)}{9\left(y+1\right)}=\frac{xy+1}{3\left(y+1\right)}\ne\frac{x+1}{3+3}=\frac{x+1}{6}\)(sai)
d)\(\frac{3xy+3x}{9y+9}=\frac{3y\left(y+1\right)}{9\left(y+1\right)}=\frac{x}{3}\)(đúng)


a) \(x^2-6x+10=\left(x^2-6x+9\right)+1=\left(x-3\right)^2+1\ge1>0\forall x\)
b) \(4x-x^2-5=-\left(x^2-4x+4\right)-1=-\left(x-2\right)^2-1\le-1< 0\forall x\)

sgk toán 8 tập 1
Bài 74. Hai đường chéo của một hình thoi bằng 8cm8cm và 10cm10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
(A) 6cm6cm; (B) √41cm41cm
(C) √164cm164cm (D) 9cm9cm ?
Bài giải:
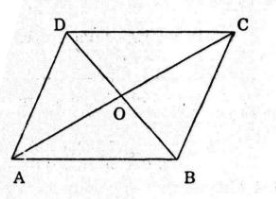
Xét bài toán tổng quát:
ABCDABCD là hình thoi, OO là giao điểm hai đường chéo.
Theo tính của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
Áp dụng định lí Pytago vào tam giác vuông ABOABO ta có:
AB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=√(12AC)2+(12BD)2=√42+52=√41cmAB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=(12AC)2+(12BD)2=42+52=41cm
Vậy (B) đúng.
Bài 79.
a) Một hình vuông có cạnh bằng 3cm3cm. Đường chéo của hình vuông đó bằng 6cm6cm, √18cm18cm, 5cm5cm hay 4cm4cm ?
b) Đường chéo của một hình vuông bằng 2dm2dm. Cạnh cảu hình vuông đó bằng: 1dm1dm,
32dm32dm, √2dm2dm hay 43dm43dm ?
Bài giải:
a) Gọi đường chéo của hình vuông có độ dài là aa.
Ta có: a2=32+32=18a2=32+32=18
Suy ra a=√18a=18
Vậy đường chéo của hình vuông đó bằng √18cm18cm.
b) Gọi cạnh của hình vuông là aa.
Ta có a2+a2=22⇒2a2=4⇒a2=2⇒a=√2a2+a2=22⇒2a2=4⇒a2=2⇒a=2
Vậy cạnh của hình vuông đó bằng √2dm2dm.

a) (a + b + c)2 = [(a + b) + c]2 = (a + b)2 + 2(a + b)c + c2
= a2+ 2ab + b2 + 2ac + 2bc + c2
= a2 + b2 + c2 + 2ab + 2bc + 2ac.
b) (a + b – c)2 = [(a + b) – c]2 = (a + b)2 - 2(a + b)c + c2
= a2 + 2ab + b2 - 2ac - 2bc + c2
= a2 + b2 + c2 + 2ab - 2bc - 2ac.
c) (a – b –c)2 = [(a – b) – c]2 = (a – b)2 – 2(a – b)c + c2
= a2 – 2ab + b2 – 2ac + 2bc + c2
= a2 + b2 + c2 – 2ab + 2bc – 2ac.
bài này phải không nếu đúng thì tích hộ mình

.
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
Tương tự HG là đường trung bình của ∆ACD.
Do đó HG // AC
Suy ra EF // HG (1)
Tương tự EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).
Cách 2: EF là đường trung bình của ∆ABC nên EF = AC.
HG là đường trung bình của ∆ACD nên HG = AC.
Suy ra EF = HG
Lại có EF // HG ( chứng minh trên)
Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3)

\(a,P=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=1\)
\(b,Q=2x^2-6x=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}\right)=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(c,M=\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
a: Ta có: \(P=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1


Với hai phân thức \(\frac{A}{B}\)và \(\frac{C}{D}\), ta tìm được hai phân thức cùng mẫu \(\frac{AD}{BD},\frac{CB}{BD}\)và thỏa mãn điều kiện :
\(\frac{AD}{BD}=\frac{A}{B},\frac{CB}{BD}=\frac{C}{D}\)
Ta nhân tử và mẫu của hai phân thức đó cùng với một đa thức \(M\ne0\), ta có hai phân thức mới cùng mẫu \(\frac{A.D.M}{B.D.M}\)và \(\frac{C.B.M}{B.D.M}\), lần lượt hai phân thức \(\frac{A}{B},\frac{C}{D}\)
Đặt \(B.D.M=E,A.D.M=A',C.B.M=C'\) ta có :
\(\frac{A'}{E}=\frac{A}{B};\frac{C'}{E}=\frac{C}{D}\)
Vì có vô số đa thức \(M\ne0\)nên ta có vô số phân thức cùng mẫu bằng phân số bài cho .
Học tốt !
lần sau mình nghĩ bạn nên tự vt đề rồi đăng lên chứ vt như bạn thì một số người lớp khác có thể bt làm nhưng lại ko bt đề để giúp bạn :))