Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ xét /\ DEF cân tại D
=> DE = DF (t/c /\ cân )
DI là trung tuyến
=> DI vuông với FE => DIE = 90* => DIF kề bù với DIE => DIF = 90* (1)
=> I là trung điểm EF
Xét /\ DIF và /\ DIE có :
DIF = DIE (cmt )
DF =DE (cmt)
IF = IE ( cmt )
=> /\ DIE = /\ DIF (c.g.c)
b/ (1) => DIE = DIF = 90*
=> 2 góc này là hai góc vuông
c/ chịu .

2) A B C D K H
a) Xét 2 tam giác DHB và tam giác DAB có:
\(\widehat{DAB}=\widehat{DHB}\)
DB là cạnh chung
\(\widehat{ABD}=\widehat{HBD}\)
\(\Rightarrow\Delta DAB=\Delta DHB\left(g-c-g\right)\)
\(\Rightarrow AD=DH\)
b) AB=BH (\(\Delta ADB=\Delta DBH\)
=> tam giác ABH cân tại B ( DB là đường p/g; đường trung tuyến )
=> \(\widehat{KDB}=\widehat{CDB}\)( \(\widehat{CDH}=\widehat{KDA}\)đối đỉnh)
=> \(\widehat{HDB}=\widehat{ADB}\)(theo câu a)
\(\Rightarrow\Delta KDA=\Delta CDH\left(g-c-g\right)\Rightarrow CH=KA\)
=> cạnh CD> cạnh AD (vì CD là cạnh huyền
c) HB=BA và CH=KA
=> KB=BC => tam giác KBC cân tại B

D E F I G M
Mình hơi lười nên chỉ cho bạn và làm tắt tí nha!
a) Vì \(\Delta DEF\) cân tại D \(\Rightarrow DE=DF\); có đường trung tuyến DI \(\Rightarrow EI=FI\)
Cùng với DI chung dễ dàng chứng minh \(\Delta DEI=\Delta DFI\left(c.c.c\right)\)\
b) Vì \(EF=10cm\Rightarrow EI=5cm\). Vì DI là đường trung tuyến của \(\Delta DEF\) cân tại D
\(\Rightarrow\widehat{DEI}=90^0\). Áp dụng ĐL Pytago vào \(\Delta DEI\Rightarrow DE=13cm\)
c) Vì G là trọng tâm \(\Delta DEF\) nên \(DG=\frac{2}{3}DI\Rightarrow IG=\frac{1}{3}DI\Leftrightarrow IG=IM\)
Vì D ; G ; I ; M thẳng hàng \(\Rightarrow\widehat{EIG}=\widehat{FIM}=90^0\). Cùng với \(EI=FI\left(cmt\right)\)
\(\Rightarrow\Delta EIG=\Delta FIM\left(c.g.c\right)\Rightarrow\widehat{EGI}=\widehat{FMI}\) ( tương ứng )
Mà 2 góc so le trong \(\Rightarrow EM//FG\left(đpcm\right)\)
Mik làm câu a
a) Xét 2 tam giác: ΔDEI và Δ DFI có: DI là cạnh chung DE=DF (2 cạnh bên của Δ cân) Vì ΔDEF là Δ cân nên DI là đường trung tuyến đồng thời là đường trung trực của EF <=> EI=IF Vậy ΔDEI =ΔDFI (c. c. c)

a) Xét ΔDEI và ΔDFI có
DE=DF(ΔDEF cân tại D)
DI chung
EI=FI(I là trung điểm của EF)
Do đó: ΔDEI=ΔDFI(c-c-c)
b) Ta có: I là trung điểm của EF(gt)
nên \(IE=IF=\dfrac{EF}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Ta có: ΔDEI=ΔDFI(cmt)
nên \(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
Áp dụng định lí Pytago vào ΔDEI vuông tại I, ta được:
\(DE^2=DI^2+IE^2\)
\(\Leftrightarrow DE^2=5^2+12^2=169\)
hay DE=13(cm)

d: Xét ΔDEF có
DI là trung tuyến
G là trọng tâm
=>DG=2/3DI=2/3*12=8cm
e: Xét ΔDEF có
G là trọng tâm
EM là trung tuyến
=>E,G,M thẳng hàng

AM là đường trung tuyến
G là trọng tâm
=> AG = 2/3 AM ( tính chất 3 đường trung tuyến )
=> AG = 2/3 . 12 = 8 ( cm )
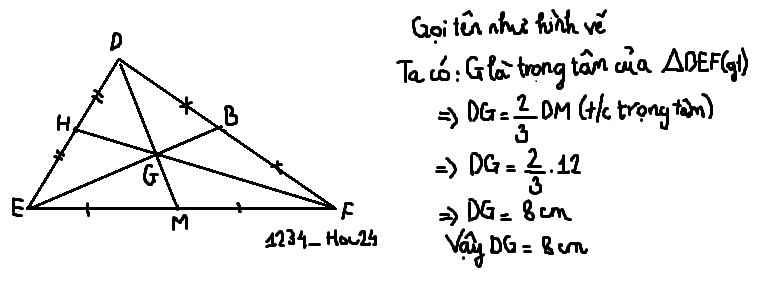
DG=2/3*DI=8cm