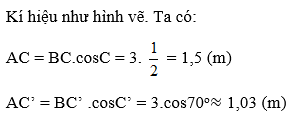Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

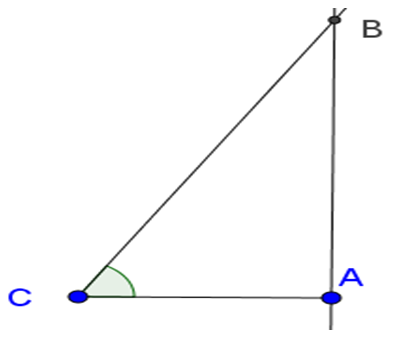
Vậy khi dùng thang, phải đặt thang cách chân tường một khoảng từ 1,03m đến 1,5 m để đảm bảo an toàn.


a, Vì SA là tiếp tuyến đường tròn (O) với A là tiếp điểm
=> ^SAO = 900 hay tam giác SAO vuông tại A
Theo định lí Pytago tam giác SAO ta có :
\(SA=\sqrt{SO^2-AO^2}=\sqrt{25-9}=4\)cm
b, Xét tam giác SAO vuông tại A, AH là đường cao
Áp dụng hệ thức : \(AH.SO=AS.AO\Rightarrow AH=\frac{AS.AO}{SO}=\frac{4.3}{5}=\frac{12}{5}\)cm
Áp dụng hệ thức : \(AO^2=HO.SO\Rightarrow HO=\frac{AO^2}{SO}=\frac{9}{5}\)cm
c, Ta có : SB = SA ( tc tiếp tuyến cắt nhau )
AO = BO = R
Vậy SO là đường trung trực đoạn AB
mà AH vuông SO => HB vuông SO
=> A;H;B thẳng hàng

a, Thay x = - 1 vảo pt trên ta được : \(1-2\left(m+1\right)+m^2-3m=0\)
\(\Leftrightarrow m^2-3m-2m-2+1=0\Leftrightarrow m^2-5m-1=0\)
\(\Delta=25-4\left(-1\right)=29>0\)
\(m_1=\frac{5-\sqrt{29}}{2};m_2=\frac{5+\sqrt{29}}{2}\)
b, Để phương trình có 2 nghiệm phân biệt : \(\Delta'=\left(m+1\right)^2-\left(m^2-3m\right)=m^2+2m+1-m^2+3m=5m-1>0\Leftrightarrow m>\frac{1}{5}\)
c, Để phương trình có nghiệm duy nhất khi \(5m-1=0\Leftrightarrow m=\frac{1}{5}\)