Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.
Suy ra: MN // BC và
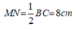
Do đó, tứ giác MNCB là hình thang .
Vì AH = 8cm nên đường cao kẻ từ M đến BC bằng
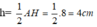
Diện tích hình thang MNCB là :
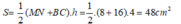
Chọn đáp án A


a)
ta có G là trọng tâm của tam giác ABC.
\(\hept{\begin{cases}\Rightarrow BH=GH=GD\\\Rightarrow EG=GK=KC\end{cases}}\)
hay G là trung điểm của EK và HD.
tứ giác EDKH có 2 đường chéo cắt nhau tại trung điểm mỗi đường
do đó tứ giác EDKH là hình bình hành.
b) để hình bình hành EDKH là hình chữ nhật thì EK=HD
⇒BD=EC⇒ΔABCcân
vậy để hình bình hành EDKH là hình chữ nhật thì tam giác ABC cân
c) vẽ đường cao AI vuông góc với BC.
khi đó AI cũng là đường trung tuyến.
\(\Rightarrow AG=\frac{2}{3}AI\)
ta có :\(\hept{\begin{cases}BE=AE\\AD=DC\end{cases}}\) nên ED là đường trung bình của tam giác ABC.
⇒\(\hept{\begin{cases}ED//BC\\2ED=BC\end{cases}}\)
vì ED//BC và AI⊥BC nên ED⊥AI
đồng thời EH⊥ED nên EH//AI.
ta có: \(\hept{\begin{cases}EH//AI\\BE=EA\end{cases}}\)\(\Rightarrow AH=\frac{AG}{2}\)
hay \(EH=\frac{\frac{2}{3}AI}{2}=\frac{1}{3}AI\Leftrightarrow3EH=AI\)
\(S\Delta ABC=\frac{AI.BC}{2}=\frac{3EH.2ED}{2}=3EH.ED\)=\(3S_{EDHK}\)
vậy\(\frac{S_{EDHK}}{S_{\Delta ABC}}=\frac{1}{3}\)
CHÚC BẠN HỌC TỐT

Bài 12:
:v Mình sửa P là trung điểm của EG
A B C D E O Q N F G M I 1 2 P
a) Ta có: \(\widehat{EAC}=\widehat{EAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{GAB}=\widehat{GAC}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\Rightarrow\widehat{EAC}=\widehat{GAB}\)
Xét tam giác EAC và tam giác BAG có:
\(\hept{\begin{cases}EA=AB\\\widehat{EAC}=\widehat{GAB}\left(cmt\right)\\AG=AC\end{cases}}\Rightarrow\Delta EAC=\Delta BAG\left(c-g-c\right)\)
\(\Rightarrow CE=BG\)( 2 cạnh t. ứng )
+) Gọi O là giao điểm của EC và BG, Gọi I là giao điểm của AC và BG
Vì \(\Delta EAC=\Delta BAG\left(cmt\right)\)
\(\Rightarrow\widehat{ACE}=\widehat{AGB}\)
Vì tam giác AIG vuông tại A nên \(\widehat{I1}+\widehat{AGB}=90^0\)(2 góc phụ nhau )
Mà \(\widehat{ACE}=\widehat{AGB}\left(cmt\right),\widehat{I1}=\widehat{I2}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{I2}+\widehat{ACE}=90^0\)
Xét tam giác OIC có \(\widehat{I2}+\widehat{ACE}+\widehat{IOC}=180^0\left(dl\right)\)
\(\Rightarrow\widehat{IOC}=90^0\)
\(\Rightarrow BG\perp EC\)
b) Vì ABDE là hình vuông (gt)
\(\Rightarrow EB\)cắt AD tại Q là trung điểm của mỗi đường (tc)
Xét tam giác EBC có Q là trung điểm của EB (cmt) , M là trung điểm của BC (gt)
\(\Rightarrow QM\)là đường trung bình của tam giác EBC
\(\Rightarrow QM=\frac{1}{2}EC\left(tc\right)\)
CMTT: \(PN=\frac{1}{2}EC;QP=\frac{1}{2}BG,MN=\frac{1}{2}BG\)
Mà EC=BG (cm câu a )
\(\Rightarrow QM=MN=NP=PQ\)
Xét tứ giác MNPQ có \(QM=MN=NP=PQ\left(cmt\right)\)
\(\Rightarrow MNPQ\)là hình thoi ( dhnb ) (1)
CM: MN//BG , QM//EC ( dựa vào đường trung bình tam giác )
Mà \(BG\perp EC\left(cmt\right)\)
\(\Rightarrow MN\perp MQ\)
\(\Rightarrow\widehat{QMN}=90^0\)(2)
Từ (1) và (2) \(\Rightarrow MNPQ\) là hình vuông ( dhnb )
\(\)
Bài 11:
A B C H D P E Q
a) Ta có: \(\widehat{HAD}+\widehat{HAE}=90^0+90^0=180^0\)
\(\Rightarrow\widehat{DAE}=180^0\)
\(\Rightarrow D,A,E\)thẳng hàng
b) Vì AHBD là hình chữ nhật (gt)
\(\Rightarrow AB\)cắt DH tại trung điểm mỗi đường (tc) và AB=DH(tc)
Mà P là trung điểm của AB (gt)
\(\Rightarrow P\)là trung điểm của DH (1)
\(\Rightarrow PH=\frac{1}{2}DH,PA=\frac{1}{2}AB\)kết hợp với AB=DH (cmt)
\(\Rightarrow PH=PA\)
\(\Rightarrow P\in\)đường trung trục của AH
CMTT Q thuộc đường trung trực của AH
\(\Rightarrow PQ\)là đường trung trực của AH
c) Từ (1) => P thuộc DH
=> D,P,H thẳng hàng
d) Vì ABCD là hình chữ nhật (gt)
=> DH là đường phân giác của góc BHA (tc) mà góc BHA= 90 độ
=> góc DHA= 45 độ
CMTT AHE =45 độ
=> góc DHA+ góc AHE=90 độ
Hay góc DHE=90 độ
=> DH vuông góc với HE
 bạn tham khảo nhé!
bạn tham khảo nhé!