Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số đô bằng nấy rùi thì yêu cầu làm gì nữa bạn
# chúc bạn học tốt #

a, xét t.giác ADB và t.giác AEC có:
AB=AC(gt)
\(\widehat{A}\)chung
=> \(\Delta\)ADB=\(\Delta\)AEC(CH-GN)
b,vì \(\widehat{B}\)=\(\widehat{C}\)(tam giác ABC cân tại A) mà \(\widehat{ABD}\)=\(\widehat{ACE}\)(theo câu a)
=>\(\widehat{OBC}\)=\(\widehat{OCB}\)
=>t.giác BOC cân tại O
c,vì AE=AD(theo câu a) suy ra t.giác AED cân tại A => \(\widehat{AED}\) =\(\widehat{ADE}\)mà t.giác ABC cx cân tại=>\(\widehat{B}\)=\(\widehat{C}\)
=> \(\widehat{AED}\)=\(\widehat{B}\)mà 2 góc này ở vị trí đồng vị nên => ED//BC
d, ta có

A B C O E D M
Cm: a) Xét t/giác ADB và t/giác AEC
có góc ADB = góc AEC = 900 (gt)
AB = AC (gt)
góc A : chung
=> t/giác ADB = t/giác AEC (ch - gn)
b) Ta có : t/goác ADB = t/giác AEC (cmt)
=> góc ABD = góc ACE (hai góc tương ứng)
Mà góc B = góc ABD + góc DBC
góc C = góc ACE + góc ECB
Và góc B = góc C (vì t/giác ABC cân)
=> góc DBC = góc ECB
hay góc OBC = góc OCB
=> t/giác BOC cân tại O
c) ta có: t/giác ADB = t/giác AEC (cm câu a)
=> AE = AD (hai cạnh tương ứng)
=> t/giác AED là t/giác cân tại A
=> góc AED = góc ADE = \(\frac{180^0-\widehat{A}}{2}\)(1)
Ta lại có: t/giác ABC cân tại A
=> góc B = góc C = \(\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) suy ra góc AED = góc ADE = góc B = góc C
Mà góc AED và góc B ở vị trí đồng vị
=> ED // BC (Đpcm)
d) ko Cm đc
A B C D E M O
a)Xét hai tam giác vuông:\(\Delta ADB\)và \(\Delta AEC\)có:
AB=AC(vì \(\Delta ABC\)cân tại A)
\(\widehat{A}\)chung
Do đó:\(\Delta ADB=\Delta AEC\)(cạnh huyền-góc nhọn)
b)Vì \(\Delta ADB=\Delta AEC\)(câu a) nênAD=AE(hai cạnh tương ứng)
Ta có:AD+DC=AC
AE+EB=AB
Mà AD=AE(cmt), AB=AC(gt)
=>DC=EB
Xét hai tam giác vuông:\(\Delta OEB\)và \(\Delta ODC\)có
EB=DC(cmt)
\(\widehat{EOB}=\widehat{DOC}\)(đối đỉnh)
Do đó: \(\Delta OEB=\Delta ODC\)(cạnh góc vuông-góc nhọn)
=>OB=OC(hai cạnh tương ứng)
=>\(\Delta BOC\)cân tại O
c)\(\Delta AED\)có AD=AE (câu b)
=>\(\Delta AED\)cân tại A
\(\Rightarrow\widehat{E}=\widehat{D}=\frac{180^0-\widehat{A}}{2}\left(1\right)\)
\(\Delta ABC\)cân tại A(gt)
\(\Rightarrow\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{D}=\widehat{C}\)
Mà hai góc này nằm ở vị trí đồng vị
=>ED//BC
Câu d bn xem lại đề bài nhé!
~~~~~~~~~~~~~~~~~~~~~~Học tốt~~~~~~~~~~~~~~~~~~~~

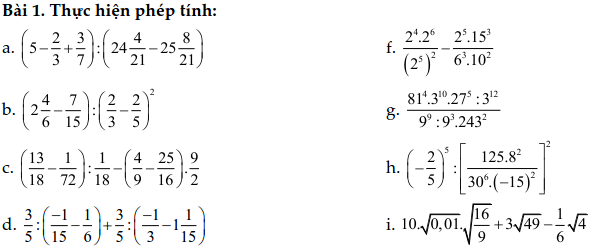
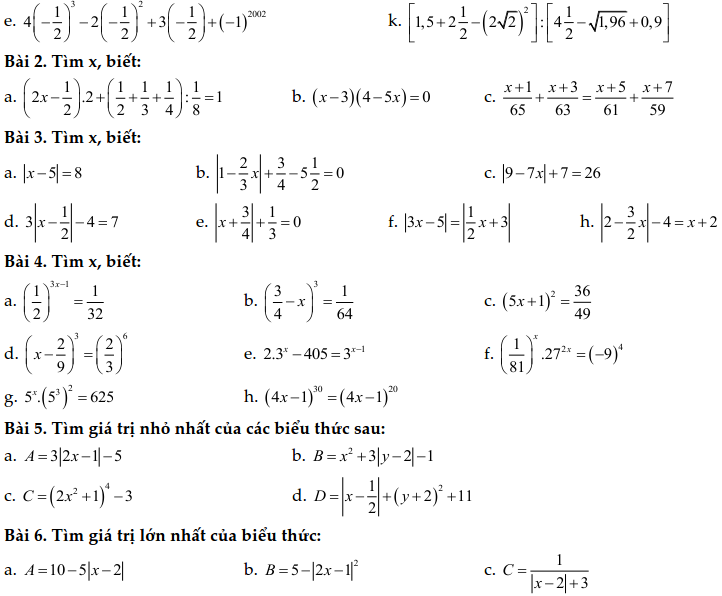
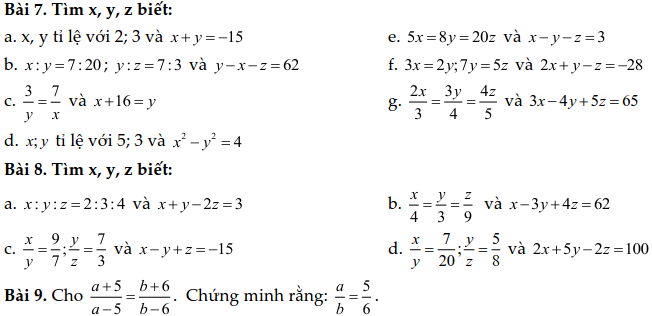
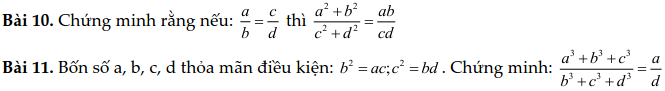 Dạng 3. Toán tỷ lệ thuận, tỷ lệ nghịch
Dạng 3. Toán tỷ lệ thuận, tỷ lệ nghịch
Gọi x là quãng đường AB ( x > 0 )
Thời gian đi : \(\dfrac{x}{50}giờ\)
Thời gian về : \(\dfrac{x}{60}giờ\)