Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải
a) Áp dụng kết quả của bài 64 chương II sách bài tập toán 7 vào ∆ABC và ∆AGB ta có:
DE // AB và DE=1/2AB (1)
IK // AB và IK=1/2AB (2)
Từ (1) và (2) suy ra: DE // IK và DE = IK
b) AD và BE là 2 đường trung tuyến của ∆ABC cắt nhau tại G.
⇒AG=2/3AD(tính chất đường trung tuyến)
Bài này dễ mà
Sử dụng tính chất đường trung tuyến của tam giác rồi CM tam giác IGK = tam giác DGE
=> IK=DE ( 2 cạnh tương ưng )
=> GIK = GDE ( 2 góc tương ứng)
Mà GIK và GDE là 2 góc so le trong
=> ....... (các bạn tự Cm nhé, Mình chỉ gợi ý như thế thôi )

a: Xét ΔABC có
D là trung điểm của BC
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//AB và DE=AB/2(1)
Xét ΔGAB có
I là trung điểm của GA
K là trung điểm của GB
Do đó: IK là đường trung bình
=>IK//AB và IK=AB/2(2)
Từ (1) và (2) suy ra DE//IK và DE=IK
b: Xét ΔABC có
AD là đường trung tuyến
BE là đường trung tuyến
AD cắt BE tại G
Do đó: G là trọng tâm của ΔABC
=>AG=2/3AD

2 đuong trung tuyen AD va BE cua tam giac ABC giao nhau tai G
vay G la trong tam cua tam giac ABC
ta co BG=AG=2/3 AD ; GE=GD=1/3 AD
ma I la trung diem cua AG: AI=IG=1/2 AG=1/3 AD
tuong tu :BK=KG=1/2 BG=1/3 AD
tu day ta co:GE=GD=IG=KG=1/3 AD
vay tam giac KGI=tam giac EGD(c-g-c)
goc KIG= goc EDG(2 goc tuong ung)
IK//DE(vi 2 goc KIG va EDG nam o vi tri so le trong)
canh IK=canh DE(2 canh tuong ung)
Vi G la trong tam cua tam giac ABC nen AG=2/3 AD(Dpcm)

tự kẻ hình nha
b) vì AD cắt BE tại G mà AD và BE là trung tuyến=> G là trọng tâm của tam giác ABC=> AG=2/3AD
a)vì G là trong tâm
=> AG=2/3AD=> GD=1/2AG
vì I là trung điểm của AG=> IG=1/2AG
=> BG=2/3BE=> GE=1/2BG
vì K là trung điểm của BG=> KG=1/2BG
xét tam giác GIK và tam gáic GDE có
IG=GD(=1/2AG)
KG=EG(=1/2BG)
IGK=EGD( đối đỉnh)
=> tam giác GIK= tam giác GDE( cgc)
=> IK=ED( hai cạnh tương ứng)
=> KIG=GDE( hai góc tương ứng)
mà KIG so le trong với GDE=> IK//ED

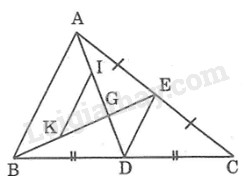
a) Áp dụng kết quả của bài 64 chương II sách bài tập toán 7 tập 1 vào \(\Delta ABC\) và vào \(\Delta AGB\) ta được:
+) \(DE\) // \(AB\) và \(DE=\frac{1}{2}AB\) (1).
+) \(IK\) // \(AB\) và \(IK=\frac{1}{2}AB\) (2).
Từ (1) và (2) => \(DE\) // \(IK\) và \(DE=IK.\)
b) Vì \(AD\) và \(BE\) là 2 đường trung tuyến của \(\Delta ABC\) cắt nhau tại G (gt).
=> \(AG=\frac{2}{3}AD\) (tính chất ba đường trung tuyến của tam giác) (đpcm).
Chúc bạn học tốt!

G A B C D E I K
Giải:
a) Ta có: \(AG=\frac{2}{3}AD\Rightarrow\frac{1}{2}AG=\frac{1}{2}.\frac{2}{3}AD\Rightarrow IG=\frac{1}{3}AD\)
\(GD=\frac{1}{3}AD\) ( tính chất đường trung tuyến )
\(\Rightarrow IG=GD\)
\(GB=\frac{2}{3}BE\Rightarrow\frac{1}{2}GB=\frac{1}{2}.\frac{2}{3}BE\Rightarrow KG=\frac{1}{3}BE\)
\(GE=\frac{1}{3}BE\) ( tính chất đường trung tuyến )
\(\Rightarrow GE=KG\)
Xét \(\Delta IKG,\Delta DEG\) có:
IG = GD ( cmt )
\(\widehat{IGK}=\widehat{EGD}\) ( đối đỉnh )
\(GK=GE\) ( cmt )
\(\Rightarrow\Delta IKG=\Delta DEG\left(c-g-c\right)\)
\(\Rightarrow IK=DE\) (
\(\Rightarrow\widehat{IKG}=\widehat{GED}\) ( góc t/ứng ) ( đpcm )
Mà 2 góc trên ở vị trí so le trong
\(\Rightarrow\)IK // DE ( đpcm )
b) Theo tính chất đường trung tuyến
\(\Rightarrow AG=\frac{2}{3}AD\left(đpcm\right)\)
Vậy...
a) Ta có E là trung điểm của AC; D là trung điểm của BC ( tính chất trung tuyến )
=> DE là đường trung bình của △ABC△ABC
=> DE // AB và DE = 1212 AB ( tính chất đường trung bình ) (1)
- Lại có I là trung điểm của AG; K là trung điểm của BG ( giả thiết )
=> IK là đường trung bình của △GAB△GAB
=> IK // AB và IK = 1212 AB ( tính chất đường trung bình ) (2)
- Từ (1) và (2) => ......................
b) Ta có AD là trung tuyến của △ABC△ABC ( giả thiết )
iiiiiziiiiiiiiiiiBE là trung tuyến của △ABC△ABC ( giả thiết )
Mà AD giao BE tại G ( giả thiết )
=> G là trọng tâm của △ABC△ABC ( tính chất trọng tâm )
=> AG = 2323 AD
uk, mk điên đó, làm gì đc mk, mk chưa học thì phải hỏi chớ, phận sự gì bn, ghét