Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

THAM KHẢO:
óm tắt:
TKHT có f = 12 cm
Vật sáng AB cao 1cm đặt vuông góc với trục chính tại A.
Khoảng cách vật – tk: d= 8 cm.
a. Vẽ ảnh A’B’ của vật AB
b. Nêu đặc điểm của ảnh.
c. Tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh.
Giải:
a. Vẽ hình minh họa sự tạo ảnh
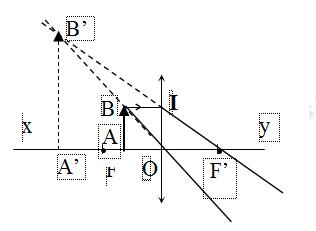
b. Vì vật nằm trong khoảng tiêu cự của thấu kính (d
c. Xét tam giác OAB và tam giác OA’B’ có: góc O chung; góc A = góc A’ = 900.
Nên tam giác OAB đồng dạng với tam giác OA’B’. Ta có các tỉ số đồng dạng:

Xét tam giác OIF’ và tam giác F’A’B’
Có:

; 
Nên tam giác OIF’ ~ tam giác F’A’B’ . Ta có tỉ số đồng dạng:

Thay số từ đề bài ta có:


Tính chất : Ảnh thật ngược chiều cao bằng vật
Ảnh cách thấu kính một đoạn là
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{4}=\dfrac{1}{6}+\dfrac{1}{d'}\Rightarrow d'=12cm\)
Chiều cao ảnh
\(h=h'=2cm\)

Mình chỉ làm phần tính toán thôi nha, còn phần vẽ thì chắc bạn cũng biết vẽ rồi
Bài Giải
a. Dựng ảnh A'B' của vật qua thấu kính ta thấy:
f < d < 2f nên ảnh A'B' là ảnh thật, ngược chiều với vật AB
b.Áp dụng công thức độ phóng đại của ảnh ta có:
\(\dfrac{AB}{A'B'}=\dfrac{d}{d'}=\dfrac{12}{24}=\dfrac{1}{2}\)
=> A'B' = 2AB =4 (cm)
Áp dụng công thức thấu kính ta có:
\(\dfrac{1}{f}\) = \(\dfrac{1}{d}+\dfrac{1}{d'}\)
=> d' = \(\dfrac{d.f}{d-f}\) = \(\dfrac{12.8}{12-8}\) = 24 (cm)

Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)

Ảnh ảo, cùng chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{15}=\dfrac{1}{10}-\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Chiều cao vật:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{6}{h'}=\dfrac{10}{30}\Rightarrow h'=18cm\)