Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: D; E lần lượt là trung điểm của OA; OB
=> DE là đường trung bình của tam giác OAB
=> DE = 1/2 AB
Chứng minh tương tự: DF = 1/2 AC; EF = 1/2 BC
=> DE + DF + EF = 1/2 AB + 1/2 AC + 1/2 BC = 1/2 (AB + AC + BC) = 1/2 . 20 = 10 cm

Xét tam giác PAC,ta có:
{MP=MAOP=OC
=>MP = 1/2 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 543/2 cm

Áp dụng định lí Ta lét đảo ta có:
\(\dfrac{OD}{OA}=\dfrac{OE}{OB}=\dfrac{OF}{OC}=\dfrac{1}{4}\Rightarrow DE\text{//}AB;EF\text{//}BC;DF\text{//}AC\\ \Rightarrow\dfrac{DE}{AB}=\dfrac{EF}{BC}=\dfrac{DF}{AC}=\dfrac{OD}{OA}=\dfrac{1}{4}\\ \Rightarrow\Delta ABC\sim\Delta DEF\left(c.c.c\right)\)
Tỉ số đồng dạng là: \(\dfrac{DE}{AB}=\dfrac{1}{4}\)

Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 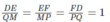
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.

Cho tam giác đều ABC diện tích 80 cm2. Dựng một tam giác vuông cân BCD như hình vẽ.

Sau đó lại lấy cạnh BD của tam giác vuông cân để dựng một tam giác đều. Cứ lặp đi lặp lại như vậy đến tam giác đều thứ 4.
Hỏi tam giác đều thứ 4 có diện tích bằng bao nhiêu?
Đáp án: 10 cm2.
Gọi cạnh tam giác đều ABC là a.
Áp dụng định lý Pytago vào tam giác vuông cân BCD ta có BD = CD = a√2/2
Nhận thấy, BD chính là cạnh của tam giác đều tiếp theo. Từ đó suy ra cạnh của tam giác đều tiếp theo luôn giảm √2/2 lần so với cạnh của tam giác đều trước đó.
Suy ra cạnh của tam giác đều thứ 4 giảm (√2/2)3 = √2/4 lần so với cạnh tam giác đầu tiên. Từ đây ta có diện tích tam giác đều thứ tư bằng (√2/4)2 = 1/8 lần so với diện tích tam giác đều đầu tiên.
Vậy diện tích tam giác đều thứ 4 bằng 80/8 = 10 cm2.

Xét tam giác PAC,ta có:
{MP=MAOP=OC{MP=MAOP=OC
=>MP = 1212 AC
Tam giác PBC và AOB tương tự
=> Tam giác MNP đồng dạng với tam giác ABC
=> Chu vi tam giác MNP = 54325432 cm
LÀM LIỀU !!
Nối M với C ; B với P ; N với A
Xét tam giác OMC có : MP là đường trung tuyến ứng với cạnh OC
=> S MOP = S MCP = 1/2. S OMC ( t/c đường trung tuyến trong tam giác )
Xét tam giác AOC có : CM là đường trung tuyến ứng với cạnh OA
=> S OCM = S ACM = 1/2. S OAC ( t/c đường trung tuyến của tam giác )
=> S OMP = 1/4.S OAC
Tương tự CM được S ONP = 1/4 S OBC ; S OMN = 1/4. S OAB
=> S OMP + S OMN + S ONP = 1/4. S OAC + 1/4. S OAB + 1/4 . S OMN
=> S MNP = 1/4. S ABC
=> S MNP / S ABC = 1/4

Lục giác DPEQFM có các cặp cạnh đối bằng nhau từng đôi một:
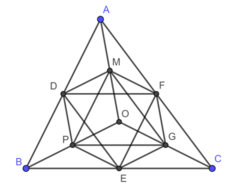
DP = QF (vì bằng 1/2 OA);
PE = MF (vì bằng 1/2 OC)
EQ = MD (vì bằng 1/2 OB)
Lục giác DPEQFM có 6 cạnh bằng nhau chỉ khi DP = PE = EQ.
Muốn vậy, ta phải có OA = OB = OC, khi đó O là điểm cách đều ba điểm A, B, C. Vậy O là giao điểm của ba đường trung trực tam giác ABC.
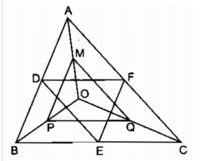
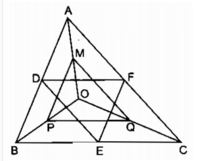
Xet ΔOAB có OD/OA=OE/OB=1/2
nên DE/AB=OD/OA=1/2
Xet ΔOAC có OD/OA=OF/OC=1/2
nên DF/AC=OD/OA=1/2
Xet ΔOBC có OE/OB=OF/OC
nên EF//BC
=>EF/BC=OE/OB=1/2
=>DE/AB=DF/AC=EF/BC
=>ΔDEF đồng dạng với ΔABC
=>\(\dfrac{S_{DEF}}{S_{ABC}}=\dfrac{1}{4}\)