Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Góc giữa B → và pháp tuyến n → là α = ( n → , B → ) = 0 ° .
ϕ = N . B . S . cos ( n → , B → ) = 1000 . B . 100 . 10 - 4 . 1 = 10 B .
e C = ∆ ϕ ∆ t = Δ Φ Δ t = | Φ 2 − Φ 1 | Δ t = 10.8.10 − 2 − 10.0 0 , 02 = 40 ( V ) .
I = e C R = 40 16 = 2 , 5 ( A ) .
Công suất toả nhiệt của ống dây: P = I 2 . R = 2 , 5 2 . 16 = 100 ( W ) .

Từ thông qua ống dây dẫn gồm N vòng dây tính bằng Φ = NBS. Vì cảm ứng từ B tăng, nên từ thông Φ tăng theo sao cho : ∆ Φ = NS ∆ B.
Áp dụng công thức của định luật Fa-ra-đây, ta xác định được độ lớn của suất điện động cảm ứng xuất hiện trong ống dây dẫn :
![]()
Từ đó suy ra cường độ dòng điện cảm ứng chạy trong ống dây dẫn :
![]()
Áp dụng định luật Jun - Len-xơ, ta tính được công suất nhiệt toả ra trong ống dây dẫn :
P = R i c 2 = 16. 25 . 10 - 3 2 = 10mW

Áp dụng công thức của định luật Fa-ra-đây về độ lớn của suất điện động cảm ứng xuất hiện trong ống dây dẫn :
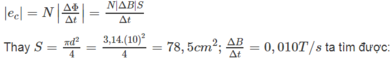
|ec|= 1000.0,010.78,5. 10 - 4 = 78,5. 10 - 4 V
Các vòng của ống dây dẫn có độ dài tổng cộng l = N π d, nên ống dây dẫn này có điện trở :
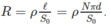
Khi nối đoản mạch hai đầu của ống dây dẫn, thì dòng điên trong ống dây dẫn có cường độ i = ec/R
Do đó, công suất toả nhiệt trên ống dây dẫn tính theo công thức :
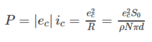
Thay số
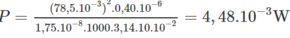

Mai dậy sớm xem bài tui làm nha :>
a/ \(\left|e_C\right|=N\left|\dfrac{\Delta\phi}{\Delta t}\right|=\dfrac{N\left|\Delta B\right|S}{\Delta t}=\dfrac{N\left|\Delta B\right|.\pi d^2}{4\Delta t}=\dfrac{1000.0,01.3,14.\left(10^{-2}\right)^2}{4}=...\left(V\right)\)
b/ \(W=\dfrac{1}{2}CU^2=\dfrac{1}{2}C.e_C^2=\dfrac{1}{2}.10^{-4}.e_C^2=...\left(J\right)\)
\(\Rightarrow Q=C.U=C.e_C=10^{-4}.e_C=...\left(C\right)\)
c/ \(l=N\pi d=1000.3,14.10^{-2}=...\left(m\right)\)
\(\Rightarrow R=\rho.\dfrac{l}{S}=1,75.10^{-8}.\dfrac{1000.3,14.10^{-2}}{0,4.10^{-6}}=...\left(\Omega\right)\)
\(i_C=\dfrac{e_C}{R}=...\left(A\right)\)
\(\Rightarrow P=e_C.i_C=...\left(W\right)\)





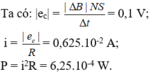

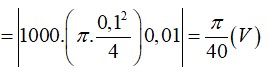
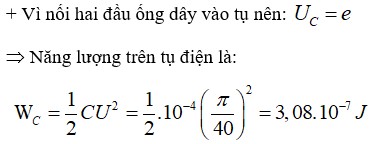
a/ \(E_c=NS\left|\frac{\Delta B}{\Delta t}\right|\cos0=1000.40.10^{-4}\left|\frac{0,06-0}{2}\right|=0,12\left(V\right)\)
b/ \(I=\frac{E_c}{R}=\frac{0,12}{4}=0,03\left(A\right)\)