Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

dự định thực tế v t s x x 3,5 x 3,5 5,25 x 5,25
Gọi độ dài quãng đường AB là x (km) (x>0)
Vận tốc của ô tô dự định đi là \(\frac{x}{3,5}\)(km/h)
Vận tốc thực tế của ô tô là \(\frac{x}{5,25}\)(km/h)
Théo đề bài ta có phương trình:
\(\frac{x}{3,5}-\frac{x}{5,25}=10\)
<=>\(\frac{3x}{10,5}-\frac{2x}{10,5}=\frac{105}{10,5}\)
<=>3x-2x=105
<=>x=105 (thỏa mãn điều kiện)
vận tốc của ô tô là:
105:5,25=20(km/h)

Giả sử ta có một phương tiện C xuất phát cùng thời điểm từ A với vận tốc bằng vận tốc trung bình của xe đạp và xe máy, khi đó C luôn luôn ở giữa xe đạp và xe máy
Vận tốc của C là
(10+30):2=20 km/h
Vấn đề đặt ra là ta tìm thời điểm ô tô gặp C thì đó chính là thời điểm ô tô ở giữa xe đạp và xe máy.
Trong cùng 1 khoảng thời gian thì vận tốc tỷ lệ thuận với quãng đường đi được
\(\frac{V_C}{V_{oto}}=\frac{S_C}{S_{oto}}=\frac{20}{60}=\frac{1}{3}\)
Quãng đường ôt tô đi đến điểm gặp nhau với C hay o tô ở giữa xe đạp và xe máy là
[120:(1+3)]x3=90 km
Thời gian ô tô ở giữa xe đạp và xe máy là
90:60=1,5 giờ
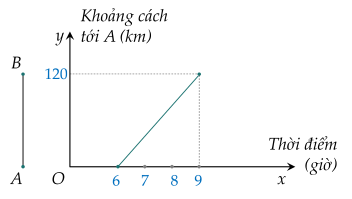
a: Đặt (d): y=ax+b
Theo đồ thị, ta sẽ thấy: (d) đi qua A(6;0) và B(9;120)
Thay x=6 và y=0 vào y=ax+b, ta được:
\(a\cdot6+b=0\)
=>6a+b=0(1)
Thay x=9 và y=120 vào y=ax+b, ta được:
\(a\cdot9+b=120\)
=>9a+b=120(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}9a+b=120\\6a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9a+b-6a-b=120\\6a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=120\\b=-6a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=40\\b=-240\end{matrix}\right.\)
b: a=40; b=-240
=>y=40x-240
Thay x=8 vào y=40x-240, ta được:
\(y=40\cdot8-240=80\left(km\right)\)
=>Ô tô còn cách B 120-80=40km