
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{16}{81}=\left(\frac{4}{9}\right)^2=\left(-\frac{4}{9}\right)^2=\left(\frac{2}{3}\right)^2=\left(-\frac{2}{3}\right)^2\)

Giải:
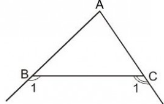
∆AHB và ∆KBH có
AH=KH ( gt )
=
BH cạnh chung .
Nên ∆AHB=∆KBH(c.g.c)
Suy ra: =
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC ( c . g . c )
Suy ra: =
Vậy CH là tia phân giác của góc C
p/s: Very làm biếng open sách so copy mạng =]]]

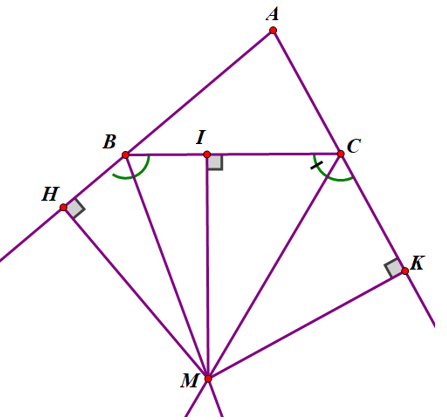
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).

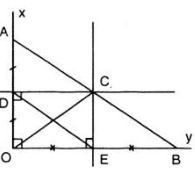
- Hình 107:
Xét \(\Delta ACD\)và \(\Delta ABD\)có:
\(\widehat{B}=\widehat{C}=90^o\left(gt\right)\)
AD là cạnh chung
\(\widehat{CAD}=\widehat{BAD}\left(gt\right)\)
\(\Rightarrow\Delta ABD=\Delta ACD\left(CH-GN\right)\)
- Hình 108:
Xét \(\Delta ACD\)và \(\Delta ABD\)có:
\(\widehat{C}=\widehat{B}=90^o\left(gt\right)\)
AD là cạnh chung
\(\widehat{CAD}=\widehat{BAD\left(gt\right)}\)
\(\Rightarrow\Delta ACD=\Delta ABD\left(CH-GN\right)\)

BAI THO BAN DEN CHOI NHA LA BAI THO HAY VIET VE TINH BAN MOT TINH BAN THAM THIET KEO SON MOT TAM HON THANH BACH CUA HAI CON NGUOI HOA LA MOT ;MOT NET SONG THANH CAO TRONG TINH TRONG NGIA TINH BAN CUA HO THAT CAM DONG; KHEP LAI BAI THO AI AI CUG XUC DONG TRUOC TINH BAN CAO QUY CUA HO



a) Đúng
b) Đúng
c) Đúng
d) Sai