Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :


Giải :
a. Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :


Đáp án A
Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :
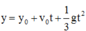
Phương trình chuyển động vật A :
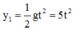
Phương trình chuyển động vật B:
![]()
![]()
Khi gặp nhau:
![]()
![]()
Suy ra t = 1,2s

a/ \(y_A=x_0+\frac{1}{2}gt^2=30-\frac{1}{2}.10t^2=30-5t^2\)
\(y_B=vt+\frac{1}{2}gt^2=25t+\frac{1}{2}.10.t^2=25t+5t^2\)
b/ \(y_A=y_B\Leftrightarrow30-5t^2=25t+5t^2\)
\(\Leftrightarrow t\approx0,87\left(s\right)\)
\(\Rightarrow y_A=26,2455\left(m\right)\)
Có \(v_A^2-v_0^2=2gS_A\Rightarrow v=23m/s\)
\(v_B^2-v_0^2=2gS_B\Rightarrow v_B=33,7\left(m/s\right)\)

\(v_0=20mm/s=0,02m/s\)
a)Đây là bài toán vật rơi tự do.
Phương trình quỹ đạo: \(y=\dfrac{g}{2v_0}x^2=\dfrac{10}{2\cdot0,02}x^2=250x^2\)
Phương trình vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{100t^2+4\cdot10^{-3}}\left(m/s\right)\)
b)Thời gian viên bi đạt độ cao cực đại:
\(v=v_0-gt\Rightarrow t=\dfrac{v-v_0}{-g}=\dfrac{0-0,02}{-10}=0,002s\)
Độ cao vật đạt cực đại:
\(H=h_0+\dfrac{v_0^2}{2g}=25+\dfrac{0,02^2}{2\cdot10}=25,00002m\)
c)Thời gian vật quay lại vị trí ban đầu sẽ bằng 2 lần thời gian vật đi đến độ cao cực đại.
\(\Rightarrow T=2t=0,004s\)
d)Thời gian viên đá rơi từ độ cao cực đại đến khi chạm đất là:
\(t'=\sqrt{\dfrac{2h_{max}}{g}}=\sqrt{\dfrac{2\cdot25,00002}{10}}\approx2,236s\)
Thời gian để bi chạm đất: \(T'=t+t'=2,238s\)
Vận tốc bi trước khi chạm đất:
\(v=\sqrt{v_0^2+\left(gt\right)^2}=\sqrt{0,02^2+\left(10\cdot2,238\right)^2}=22,38m/s\)
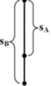
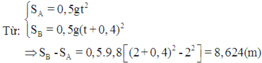
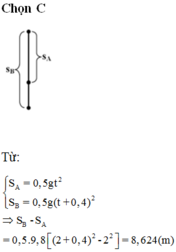
Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :
Gòi k đánh nổi chữ tham khảo hay j :)