Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : V = 1313.S.h = 1313.4.2 = 8383
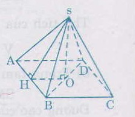
b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
SH2 = SO2 + OH2 = SO2+ (BC2)2(BC2)2 = 22 + 12 = 5
SH = √5 ≈ 2,24m
Nên Sxq = p.d = 1212 2.4.2.24 = 8,96 (m2)
Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : \(V=\dfrac{1}{3}.S.h=\dfrac{1}{3}.4.2=\dfrac{8}{3}\)

b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
\(SH^2=SO^2+OH^2=SO^2+\left(\dfrac{BC}{2}\right)^2=2^2+1^2=5\)
\(SH=\sqrt{5}\approx2,24m\)
Nên Sxq = p.d = \(\dfrac{1}{2}\) 2.4.2.24 = 8,96 (m2)

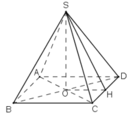
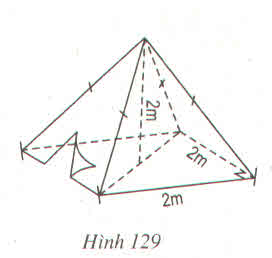
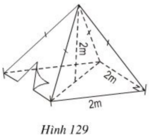
a) Lều là hình chóp đều có đáy là hình vuông cạnh bằng 2m, chiều cao bằng 2m.
Thể tích không khí trong lều bằng thể tích lều và bằng:
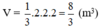
b) Số vải bạt cần thiết đề dựng lều chính là diện tích xung quanh của lều.
Dựng trung đoạn SH.
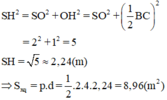

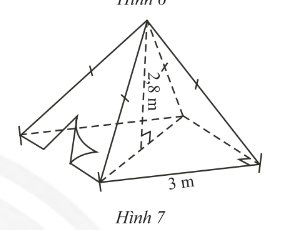
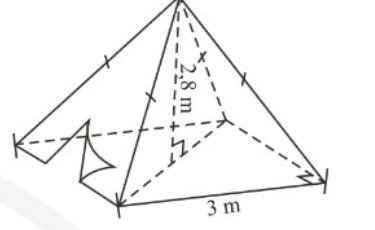
a) Thể tích không khí trong chiếc lều là: \(\frac{1}{3}{.3^2}.2,8 = 8,4\) (\({m^3}\))
b) Độ dài trung đoạn của hình chóp là: \(\sqrt {2,{8^2} + 1,{5^2}} \approx 3,18\)
Diện tích vải lều là: \(\frac{{4.3}}{2}.3,18= 19,08\) (\(c{m^2}\))

Diện tích vải lều cần phủ kín các mặt bên:
S = 4 . 3 . 3,2 : 2 = 19,2 (m²)

a) Tính được diện tích bạt phủ 2 mái lều: 20 (m2)
b) Thể tích của leeud trại là: V = 12 (m3)

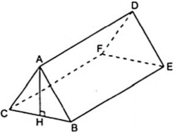
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có: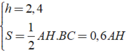
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )

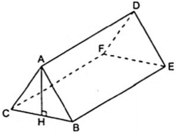
Áp dụng công thức thể tích của hình lăng trụ đứng ta có: V = S.h
Ta có: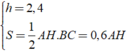
Do đó: V = S.h = 0,6AH.2,4 = 1,44AH
Theo giả thiết ta có: 1,44AH = 2,16 ⇔ AH = 1,5( cm )

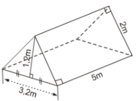
a) Lều là lăng trụ đứng tam giác.
Diện tích đáy (tam giác):
S=12.3,2.1,2=1,92(m2)S=12.3,2.1,2=1,92(m2)
Thể tích khoảng không bên trong lều là:
V = Sh = 1,92. 5 = 9,6 (m3)
b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.
Diện tích xung quanh lăng trụ là:
Sxq = 2ph = (2 + 2+ 3,2) .5 = 36 (m2)
Diện tích toàn phần:
Stp = Sxq + 2Sđ = 36 + 2.1,92 = 39,84 (m2)
Diện tích mặt bên kích thước 5m và 3,2m là:
S = 5.3,2 = 16 (m2)
Vậy số vải bạt cần có để dựng lều là:
39,84 – 16 = 23,84 (m2)
Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.



Bài 3,4: Bạn cho mình xin hình vẽ nha bạn
Bài 5:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b:
Sửa đề: Chứng minh BMED là hình bình hành
Xét ΔABC có
M là trung điểm của BC
MD//AC(Cùng vuông góc với AB)
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB(cùng vuông góc với AC)
Do đó: E là trung điểm của AC
Xét ΔABC có
E,M lần lượt là trung điểm của CA,CB
=>EM là đường trung bình của ΔABC
=>EM//AB và \(EM=\dfrac{AB}{2}\)
Ta có: EM//AB
D\(\in\)AB
Do đó: EM//BD
Ta có: \(EM=\dfrac{AB}{2}\)
\(DB=\dfrac{AB}{2}\)
Do đó: EM=BD
Xét tứ giác EMBD có
EM//BD
EM=BD
Do đó: EMBD là hình bình hành
c: Xét tứ giác AMBN có
D là trung điểm chung của AB và MN
=>AMBN là hình bình hành
Hình bình hành AMBN có MN\(\perp\)AB
nên AMBN là hình bình hành
=>AB là phân giác của góc MAN
=>\(\widehat{MAN}=2\cdot\widehat{MAB}\)
Xét tứ giác AMCP có
E là trung điểm chung của AC và MP
=>AMCP là hình bình hành
Hình bình hành AMCP có AC\(\perp\)MP
nên AMCP là hình thoi
=>AC là phân giác của góc MAP
=>\(\widehat{MAP}=2\cdot\widehat{MAC}\)
Ta có: \(\widehat{MAP}+\widehat{MAN}=\widehat{PAN}\)
=>\(\widehat{PAN}=2\cdot\left(\widehat{MAB}+\widehat{MAC}\right)\)
=>\(\widehat{PAN}=2\cdot\widehat{BAC}=180^0\)
=>P,A,N thẳng hàng