Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{A}{B}=\dfrac{3x^4+3x^2+x^3+x-3x^2-3+5x-2}{x^2+1}=3x^2+x-3+\dfrac{5x-2}{x^2+1}\)
Để A chia hết cho B thì \(\left(5x-2\right)\left(5x+2\right)⋮x^2+1\)
\(\Leftrightarrow25x^2-4⋮x^2+1\)
\(\Leftrightarrow25x^2+25-29⋮x^2+1\)
\(\Leftrightarrow x^2+1\in\left\{1;29\right\}\)
hay \(x\in\left\{0;2\sqrt{7};-2\sqrt{7}\right\}\)

A B C O D H P Q I
a. Xét tứ giác ADOH có:\(\widehat{ODA}=90^o;\widehat{DAH}=90^o;\widehat{OHA}=90^o\)
\(\Rightarrow\) ADOH là hình chữ nhật ( tứ giác có 3 góc vuông )
b. Ta có: P là điểm đối cứng của D qua O ⇒ O là trung điểm của DP(1)
Q là điểm đối xứng của H qua O ⇒ O là trung điểm của QH(2)
Ta có: \(AB\perp AC;QH\perp AC̸\) ⇒ AB//QH
Lại có: DB//QO;DB⊥DP⇒QH⊥DP(3)
Từ(1),(2),(3)⇒Tứ giác QDHP là hình thoi(Tứ giác có 2 đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường)

Bài 1: Giải: Xét tam giác ACD có F,G lần lượt là trung điểm AC,DC nên FG là đường trung bình
\(\Rightarrow\)\(FG//AD\)
C/m tương tự đc \(EH//AD; GH//EF//BC\)
\(\Rightarrow EFGH\) là hình bình hành
a/Để EFGH là hình chữ nhật thì góc \(FGH=90^o\)
\(\Rightarrow góc HGD+góc FGC=90^o\)
Mà góc HGD=góc BCD;góc FGC= góc ADC ( góc đồng vị = nhau)
\(\Rightarrow\) góc BCD+góc ADC=\(90^o\)
\(\Rightarrow\)Để EFGH là hình chữ nhật thì tứ giác ABCD cần có góc BCD+góc ADC=\(90^o\)
b/Để EFGH là hình thoi thì FG=HG
Mà FG=1/2AD; HG=1/2BC
\(\Rightarrow\)AD=BC
\(\Rightarrow\)Để EFGH là hình thoi thì tứ giác ABCD có AD=BC
c/ để EFGH là hình vuông thì EFGH phải vừa là hình chữ nhật vừa là hình thoi\(\Rightarrow \)ABCD phải có đủ cả 2 điều kiện trên

Kẻ IG,IK,IH lần lượt vuông góc với AB,BC,AC
Kẻ MO,MD,ME lần lượt vuông góc với AB,BC,AC
Xét ΔBKI vuông tại K và ΔBGI vuông tại G có
BI chung
góc KBI=góc GBI
Do đó: ΔBKI=ΔBGI
Suy ra: IK=IG(1)
Xét ΔCKI vuông tại K và ΔCHI vuông tại H có
CI chung
góc KCI=góc HCI
Do dó: ΔCKI=ΔCHI
Suy ra: IK=IH(2)
Từ (1) và (2) suy ra IG=IH
mà I nằm trong ΔABC và IG,IH là các đường cao ứng với các cạnh AB,AC
nên AI là phân giác của góc BAC(3)
Xét ΔBOM vuông tại O và ΔBDM vuông tại D có
BM chung
góc OBM=góc DBM
Do đó: ΔBOM=ΔBDM
Suy ra: MO=MD(4)
Xét ΔMDC vuông tại D và ΔMEC vuông tại E có
CM chung
góc DCM=góc ECM
Do đó: ΔMDC=ΔMEC
Suy ra: MD=ME(5)
Từ (4) và (5) suy ra MO=ME
mà M nằm ngoài ΔABC và MO,ME là các đường cao ứng với các cạnh AB,AC
nên AM là phân giác của góc BAC(6)
Từ (3) và (6) suy ra A,I,M thẳng hàng
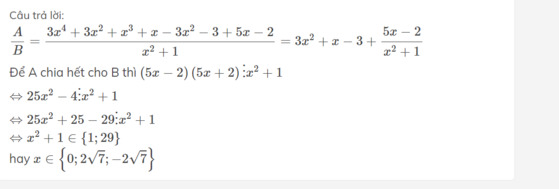
A B C M H D G O
Xét tứ giác BHCD có
MH=MD; MB=MC => BHCD là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành)
=> BD//CH
mà \(CH\perp AB\) (H là trực tâm => CH là đường cao của tg ABC)
\(\Rightarrow BD\perp AB\Rightarrow\widehat{ABD}=90^o\)
b/ Ta có BHCD là hình bình hành => CD//BH
H là trực tâm của tg ABC => BH là đường cao của tg ABC \(\Rightarrow BH\perp AC\)
\(\Rightarrow CD\perp AC\Rightarrow\widehat{ACD}=90^o\) => C thuộc đường tròn đường kính AD tâm O
Ta có \(\widehat{ABD}=90^o\left(cmt\right)\) => B thuộc đường tròn đường kính AD tâm O
=> A; B;C cùng nằm trên đường tròn đường kính AD tâm O nên O là tâm đường tròn ngoại tiếp tg ABC
c/
Xet tg AHD có
OA=OD; MH=MD => OM là đường trung bình của tg AHD \(\Rightarrow\frac{OM}{AH}=\frac{1}{2}\)
=> OM//AH
Xét tg AHG và tg MOG có
\(\widehat{HAG}=\widehat{OMG}\) (góc so le trong)
\(\widehat{AGH}=\widehat{MGO}\) (Góc đối đỉnh)
=> tg AHG đồng dạng với tg MOG \(\Rightarrow\frac{MG}{GA}=\frac{OM}{AH}=\frac{1}{2}\Rightarrow\frac{MG}{AM}=\frac{1}{3}\)
Mà O thuộc trung tuyến AM của tg ABC
=> O là trọng tâm của tg ABC