Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A: M, Fe\\ A+H_2SO_4 \to ASO_4+H_2\\ n_{H_2}=\frac{5,376}{22,4}=0,24(mol)\\ n_A=n_{H_2}=0,24(mol)\\ M_A=\frac{12}{0,24}=50(g/mol)\\ A+2HCl \to ACl_2+H_2\\ n_A=\frac{1}{2}.n_{HCl}=\frac{1}{2}.0,24=0,12(mol)\\ M_A=\frac{3,6}{0,12}=30(g/mol)\\ 30< A <50\\ a/ \\\Rightarrow A: Ca\\ b/ \\ Fe+H_2SO_4 \to FeSO_4+H_2\\ Ca+H_2SO_4 \to CaSO_4+H_2\\ n_{Fe}=a(mol)\\ n_{Ca}=b(mol)\\ m_{hh}=56a+40b=12(1)\\ n_{H_2}=a+b=0,24(mol)(2)\\ (1)(2)\\ a=0,15\\ b=0,09\\ \%m_{Fe}=\frac{0,15.56}{12}.100\%=70\%\\ \%m_{Ca}=100\%-70\%=30\% \)

a, Ta có: \(n_{H_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
PT: \(M+H_2SO_4\rightarrow MSO_4+H_2\)
Theo PT: \(n_M=n_{H_2}=0,2\left(mol\right)\)
\(\Rightarrow M_M=\dfrac{11,2}{0,2}=56\left(g/mol\right)\)
→ M là Fe.
b, Theo PT: \(n_{FeSO_4}=n_{H_2SO_4\left(pư\right)}=n_{H_2}=0,2\left(mol\right)\)
⇒ nH2SO4 dư = 0,5.1 - 0,2 = 0,3 (mol)
\(\Rightarrow\left\{{}\begin{matrix}C_{M_{H_2SO_4\left(dư\right)}}=\dfrac{0,3}{0,5}=0,6\left(M\right)\\C_{M_{FeSO_4}}=\dfrac{0,2}{0,5}=0,4\left(M\right)\end{matrix}\right.\)
c, Ta có: \(n_{FeSO_4.7H_2O}=n_{FeSO_4}=0,2\left(mol\right)\)
\(\Rightarrow m_{FeSO_4.7H_2O}=0,2.278=55,6\left(g\right)\)

nH2 = 1,344 : 22,4 = 0,06(mol)
pthh 2M+ 3H2SO4 ---> M2(SO4)3+ 3H2
0,04<-- 0,06---------------------------0,06(mol)
M M = 1,08 : 0,04 = 27 (g/mol )
=> M : Al
mH2SO4 = 0,06.98 =5,88 (g)
nH2 = 1,344/22,4 = 0,06 (mol)
PTHH:
2M + 3H2SO4 -> Al2(SO4)3 + 3H2
0,04 <--- 0,06 <--- 0,02 <--- 0,06
M(M) = 1,08/0,04 = 27 (g/mol(
=> M là Al
mH2SO4 = 0,06 . 98 = 5,88 (g)

\(n_{Fe} = a(mol) ; n_M = b(mol)\\ \Rightarrow 56a + Mb = 12\)
\(Fe + 2HCl \to FeCl_2 + H_2\\ M + 2HCl \to MCl_2 + H_2\\ n_{H_2} = a + b = \dfrac{4,48}{22,4} = 0,2(mol)\\ \Rightarrow a = 0,2 - b ( 0< b < 0,2)\)
Suy ra:
56(0,2 - b) + Mb = 12
\(\Rightarrow M = \dfrac{0,8 + 56b}{b}\)
Vì 0 < b < 0,12
Nên M > 62,67(1)
Mặt khác,
\(n_M > \dfrac{1}{2}n_{HCl} = 0,35\\ \Rightarrow M < \dfrac{23,8}{0,35} = 68(2)\)
Từ (1)(2) suy ra: 62,67 < M < 68
Do đó, M = 65(Zn) thì thỏa mãn
Vậy M là Zn(Kẽm)

a) Do dd sau pư có 3 chát tan với nồng độ % bằng nhau
=> \(m_{Al_2\left(SO_4\right)_3}=m_{ZnSO_4}=m_{H_2SO_4\left(dư\right)}\)
Gọi số mol Al, Zn là a, b (mol)
PTHH: 2Al + 3H2SO4 --> Al2(SO4)3 + 3H2
a----->1,5a------->0,5a----->1,5a
Zn + H2SO4 --> ZnSO4 + H2
b----->b--------->b----->b
=> \(\left\{{}\begin{matrix}m_{Al_2\left(SO_4\right)_3}=342.0,5a=171a\left(g\right)\\m_{ZnSO_4}=161b\left(g\right)\end{matrix}\right.\)
=> 171a = 161b
=> \(\dfrac{a}{b}=\dfrac{161}{171}\) (1)
Có: \(\dfrac{m_{Al}}{m_{Zn}}=\dfrac{27.n_{Al}}{65.n_{Zn}}=\dfrac{27}{65}.\dfrac{161}{171}=\dfrac{483}{1235}\)
b) \(n_{H_2}=1,5a+b=\dfrac{11,2}{22,4}=0,5\left(mol\right)\) (2)
(1)(2) => \(\left\{{}\begin{matrix}a=\dfrac{161}{825}\left(mol\right)\\b=\dfrac{57}{275}\left(mol\right)\end{matrix}\right.\)
=> \(x=\dfrac{161}{825}.27+\dfrac{57}{275}.65=\dfrac{5154}{275}\left(g\right)\)
\(m_{H_2SO_4\left(dư\right)}=m_{Al_2\left(SO_4\right)_3}=342.0,5\dfrac{161}{825}=\dfrac{9177}{275}\left(g\right)\)
=> \(m_{H_2SO_4\left(bđ\right)}=98\left(1,5a+b\right)+\dfrac{9177}{275}=\dfrac{22652}{275}\left(g\right)\)
=> \(y=\dfrac{\dfrac{22652}{275}.100}{10}=\dfrac{45304}{55}\left(g\right)\)

a) Do dd sau pư có 3 chát tan với nồng độ % bằng nhau
=> \(m_{Al_2\left(SO_4\right)_3}=m_{ZnSO_4}=m_{H_2SO_4\left(dư\right)}\)
Gọi số mol Al, Zn là a, b (mol)
PTHH: 2Al + 3H2SO4 --> Al2(SO4)3 + 3H2
a----->1,5a------->0,5a----->1,5a
Zn + H2SO4 --> ZnSO4 + H2
b----->b--------->b----->b
=> \(\left\{{}\begin{matrix}m_{Al_2\left(SO_4\right)_3}=342.0,5a=171a\left(g\right)\\m_{ZnSO_4}=161b\left(g\right)\end{matrix}\right.\)
=> 171a = 161b
=> \(\dfrac{a}{b}=\dfrac{161}{171}\) (1)
Có: \(\dfrac{m_{Al}}{m_{Zn}}=\dfrac{27.n_{Al}}{65.n_{Zn}}=\dfrac{27}{65}.\dfrac{161}{171}=\dfrac{483}{1235}\)
b) \(n_{H_2}=1,5a+b=\dfrac{11,2}{22,4}=0,5\left(mol\right)\) (2)
(1)(2) => \(\left\{{}\begin{matrix}a=\dfrac{161}{825}\left(mol\right)\\b=\dfrac{57}{275}\left(mol\right)\end{matrix}\right.\)
=> \(x=\dfrac{161}{825}.27+\dfrac{57}{275}.65=\dfrac{5154}{275}\left(g\right)\)
\(m_{H_2SO_4\left(dư\right)}=m_{Al_2\left(SO_4\right)_3}=342.0,5\dfrac{161}{825}=\dfrac{9177}{275}\left(g\right)\)
=> \(m_{H_2SO_4\left(bđ\right)}=98\left(1,5a+b\right)+\dfrac{9177}{275}=\dfrac{22652}{275}\left(g\right)\)
=> \(y=\dfrac{\dfrac{22652}{275}.100}{10}=\dfrac{45304}{55}\left(g\right)\)

Giả sử \(\left\{{}\begin{matrix}n_{Al}=a\left(mol\right)\\n_M=1,5a\left(mol\right)\end{matrix}\right.\)
=> 27a + MM.1,5a = 6,3 (g) (1)
\(n_{H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\)
- TH1: Nếu M không tác dụng với dd HCl
PTHH: 2Al + 6HCl --> 2AlCl3 + 3H2
0,2<------------------0,3
=> a = 0,2 (mol)
(1) => MM = 3 (L)
- TH2: Nếu M tác dụng với dd HCl
PTHH: 2Al + 6HCl --> 2AlCl3 + 3H2
a----------------------->1,5a
M + 2HCl --> MCl2 + H2
1,5a---------------->1,5a
=> 1,5a + 1,5a = 0,3
=> a = 0,1
(1) => MM = 24 (g/mol)
=> M là Mg
\(\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,1.27}{6,3}.100\%=42,857\%\\\%m_{Mg}=\dfrac{0,15.24}{6,3}.100\%=57,143\%\end{matrix}\right.\)

\(R+H_2SO_4\rightarrow RSO_4+H_2\\ n_{H_2}=\dfrac{7,168}{22,4}=0,32\left(mol\right)\\ n_R=n_{H_2}=0,32\left(mol\right)\\ M_R=\dfrac{7,68}{0,32}=24\left(\dfrac{g}{mol}\right)\\ \Rightarrow R\left(II\right):Magie\left(Mg=24\right)\)
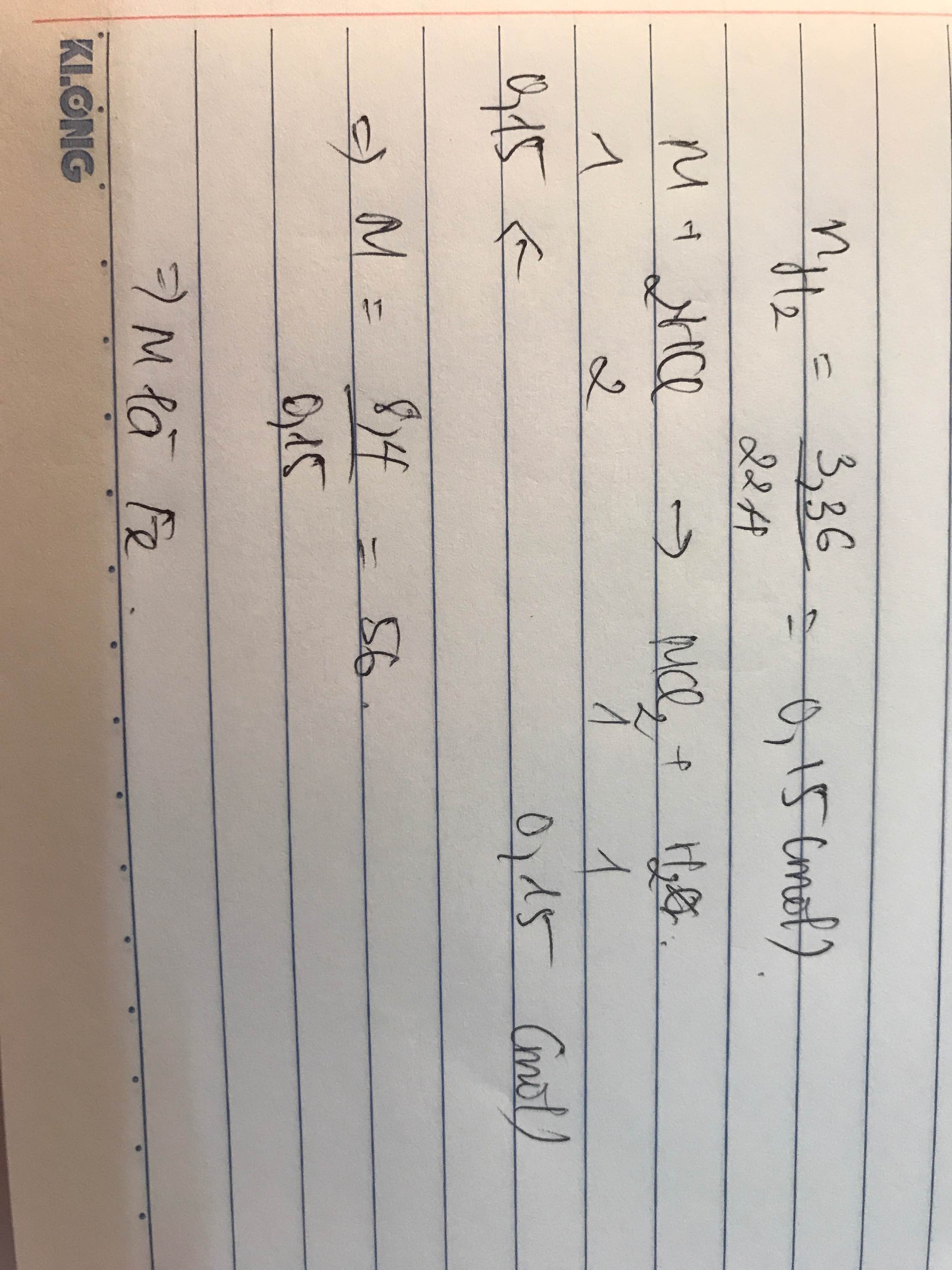
1. PTHH : M + H2SO4 -> MSO4 + H2
2. \(n_{H_2}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
\(M_M=\dfrac{m}{n}=\dfrac{3,6}{0,15}=24\left(\dfrac{g}{mol}\right)\)
=> M là nguyên tử Mg