Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

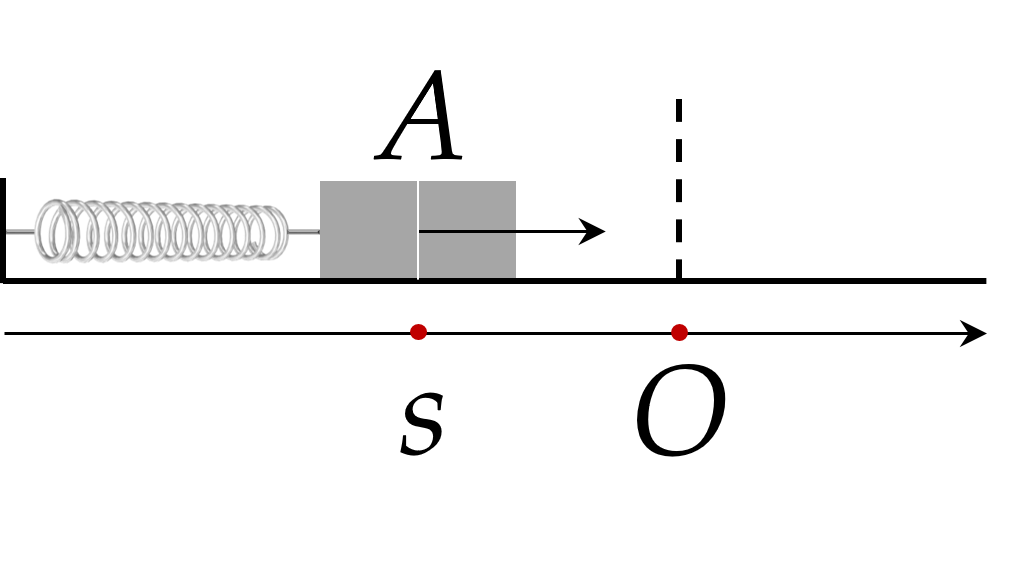
Khi: \(s = - 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = - \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = - \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.

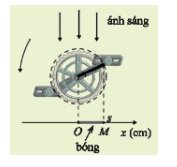
Độ dài bóng OM bằng 10 cm khi s = 10 hoặc s = -10.
Khi s = 10. Ta có: \(17cos5\pi t = 10 \Leftrightarrow cos5\pi t = \frac{{10}}{{17}}\)
Khi s = 10. Ta có: \(17cos5\pi t = - 10 \Leftrightarrow cos5\pi t = \frac{{ - 10}}{{17}}\)
Từ đó, ta có thể xác định được các thời điểm t bằng cách giải phương trình côsin.

Ta có: \(s\in\left[-1;1\right]\Leftrightarrow-1\le2cos\left(\pi t\right)\le1\\ \Leftrightarrow-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\)
Trong 1s đầu tiên \(0< t< 1\Rightarrow0< \pi t< \pi\)
Ta có đồ thị hàm số \(y=cos\left(x\right)\) trên \(\left[0;\pi\right]\)
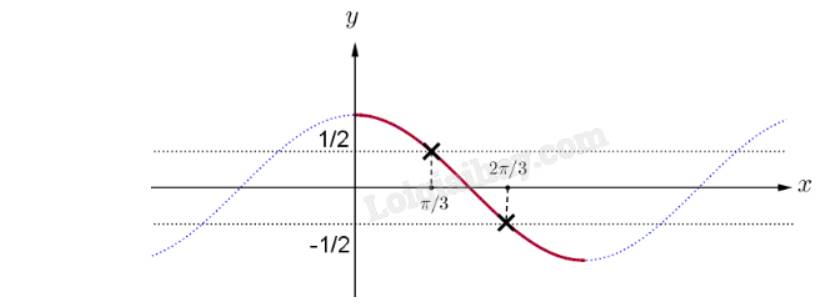
Dựa vào đồ thị, ta thấy
\(-\dfrac{1}{2}\le cos\left(\pi t\right)\le\dfrac{1}{2}\Leftrightarrow\dfrac{\pi}{3}\le\pi t\le\dfrac{2\pi}{3}\Leftrightarrow\dfrac{1}{3}\le t\le\dfrac{2}{3}\)
Vậy \(t\in\left[\dfrac{1}{3};\dfrac{2}{3}\right]\)

Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.

Trả lời:
a) Vận tốc của chuyển động khi t = 2 (s).
Ta có:
v=dsdt=S′=3t2−6t−9v=dsdt=S′=3t2−6t−9
Khi t = 2(s) ⇒ 3.22 – 6.22 – 9 = -9 m/s.
b) Gia tốc của chuyển động khi t = 3(s). Ta có:
a=dvdt=v′=6t−6a=dvdt=v′=6t−6
Ở t = 3(s) ⇒ a = 6.3 – 6 = 12 m/s2
c) Ta có: v = 3t2 – 6t – 9
Tại thời điểm vận tốc triệt tiêu:
v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)
Gia tốc: a = 6t – 6.
Khi t = 3s ⇒ a = 6.3 – 6 = 12 m/s2
d) Ta đã có a = 6t – 6.
Khi a = 0 ⇔ 6t – 6= 0 ⇔ t = 1(s)
Lại có: v = 3t2 – 6t – 9
Khi t = 1(s) ⇒ v = 3.12 – 6.1 – 9 = -12 m/s

Vận tốc tại thời điểm t là \(v\left( t \right) = s'\left( t \right) = 0,5.2\pi \cos \left( {2\pi t + \frac{\pi }{5}} \right) = \pi \cos \left( {2\pi t + \frac{\pi }{5}} \right)\)
Gia tốc tức thời của vật tại thời điểm t là \(a\left( t \right) = v'\left( t \right) = - \pi .2\pi \sin \left( {2\pi t + \frac{\pi }{5}} \right) = - 2{\pi ^2}\sin \left( {2\pi t + \frac{\pi }{5}} \right)\)
Tại thời điểm t = 5 giây, gia tốc của vật là \(a\left( 5 \right) = - 2{\pi ^2}\sin \left( {2\pi .5 + \frac{\pi }{5}} \right) \approx - 11,6\)(cm/s2)

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
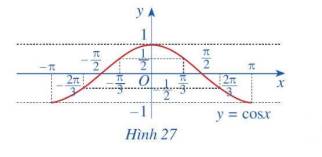
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
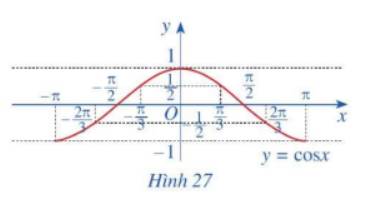
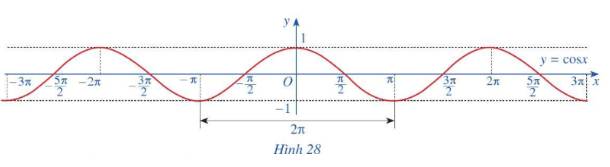
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.

$[v(t) = \frac{ds(t)}{dt} = \frac{d}{dt}(2t^3+4t+1)]$
$[a(t) = \frac{dv(t)}{dt} = \frac{d}{dt}(6t^2 + 4)]$
$[a(t) = 12t]$
Khi (t = 1), ta có:
$[v(1) = 6(1)^2 + 4 = 10 , \text{m/s}]$4
$[a(1) = 12(1) = 12 , \text{m/s}^2]$
Vậy, khi (t = 1), vận tốc của vật là 10 m/s và gia tốc của vật là $12 m/s$

Xét phương trình \(\left| {17cos5\pi t} \right| = 10\)
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}17cos5\pi t = 10\\17cos5\pi t =-10\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}cos5\pi t = \frac{{10}}{{17}}\\cos5\pi t = -\frac{{10}}{{17}}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}5\pi t = \pm 0,9 + k2\pi \\5\pi t = \pm 2,2 + k2\pi \end{array} \right.\left( {k\; \in \;\mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}t = \pm 0,06 + k\frac{2}{5}\\t = \pm 0,14 + k\frac{2}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Độ dài bóng \(|x|\;\)bằng 10 cm tại các thời điểm \(t = \pm 0,06 + k\frac{2}{5}\),\(t = \pm 0,14 + k\frac{2}{5}\),\(k \in \mathbb{Z}\).