Để x là căn bậc hai số học của số a không âm là x ≥ a và x2 = a.
Ví dụ 2 là căn bậc hai số học của 4 vì 2 > 0 và 22 = 4.
2 (trang 39 SGK Toán 9 Tập 1): Chứng minh √a2 = |a| với mọi số a.
Trả lời:

3 (trang 39 SGK Toán 9 Tập 1): Biểu thức A phải thỏa mãn điều kiện gì để √A xác định prôtêin
Trả lời:
√A xác định khi A > 0 hay nói cách khác : điều kiện xác định của căn bậc hai là biểu thức lấy căn không âm.
4 (trang 39 SGK Toán 9 Tập 1): Phát biểu và chứng minh định lí về mối liên hệ giữa phép nhân và phép khai phương. Cho ví dụ.
Trả lời:
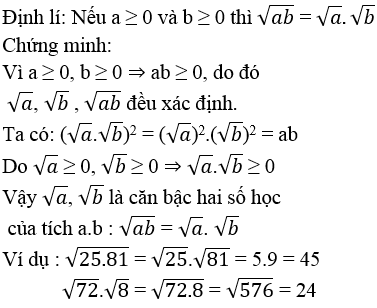
5 (trang 39 SGK Toán 9 Tập 1): Phát biểu và chứng minh định lí về mối liên hệ giữa phép chia và phép khai phương. Cho ví dụ.
Trả lời:
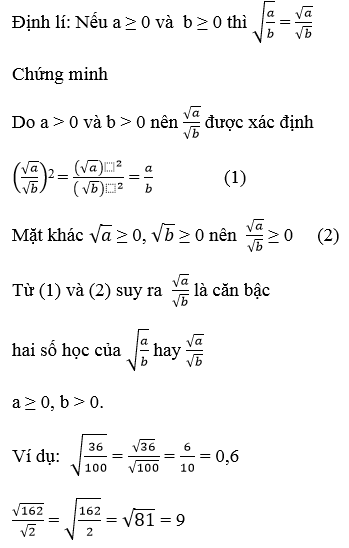
Tham khảo lời giải các bài tập Toán 9 bài ôn tập chương I khác:
Câu hỏi ôn tập Chương 1 (trang 39 SGK Toán 9 Tập 1):1. Nêu điều kiện để x là căn bậc hai ... 2. Chứng minh √a2 = |a| ...
Bài 70 (trang 40 SGK Toán 9 Tập 1):Tìm giá trị các biểu thức sau bằng cách...
Bài 71 (trang 40 SGK Toán 9 Tập 1):Rút gọn các biểu thức sau:...
Bài 72 (trang 40 SGK Toán 9 Tập 1):Phân tích thành nhân tử (với các số...
Bài 73 (trang 40 SGK Toán 9 Tập 1):Rút gọn rồi tính giá trị các biểu thức sau:...
Bài 74 (trang 40 SGK Toán 9 Tập 1):Tìm x, biết:...
Bài 75 (trang 40 SGK Toán 9 Tập 1):Chứng minh các đẳng thức sau:...
Bài 76 (trang 41 SGK Toán 9 Tập 1):Cho biểu thức...
Mục lục Giải bài tập Toán 9 theo chương:
- Tập 1
- Chương I: Căn Bậc Hai. Căn Bậc Ba
- Chương II: Hàm Số Bậc Nhất
- Chương I: Hệ Thức Lượng Trong Tam Giác Vuông
- Chương II: Đường Tròn
- Tập 2
- Chương III: Hệ Hai Phương Trình Bậc Nhất Hai Ẩn
- Chương IV: Hàm Số y = ax2 (a ≠ 0) - Phương Trình Bậc Hai Một Ẩn
- Chương III: Góc Với Đường Tròn
- Chương IV: Hình Trụ - Hình Nón - Hình Cầu
Đã có app VietJack trên điện thoại, giải bài tập SGK, soạn văn, văn mẫu.... Tải App để chúng tôi phục vụ tốt hơn.
Tải App cho Android hoặc Tải App cho iPhone
Loạt bài Giải bài tập Toán lớp 9 | Để học tốt Toán 9 của chúng tôi được biên soạn bám sát theo chương trình Sách giáo khoa Toán 9 (Tập 1 & Tập 2) và một phần dựa trên quyển sách Giải bài tập Toán 9 và Để học tốt Toán lớp 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
Trang trước
Trang sau
Các loạt bài lớp 9 khác
- Soạn Văn 9
- Soạn Văn 9 (bản ngắn nhất)
- Văn mẫu lớp 9
- Đề kiểm tra Ngữ Văn 9 (có đáp án)
- Giải bài tập Toán 9
- Giải sách bài tập Toán 9
- Đề kiểm tra Toán 9
- Đề thi vào 10 môn Toán
- Chuyên đề Toán 9
- Giải bài tập Vật lý 9
- Giải sách bài tập Vật Lí 9
- Giải bài tập Hóa học 9
- Chuyên đề: Lý thuyết - Bài tập Hóa học 9 (có đáp án)
- Giải bài tập Sinh học 9
- Giải Vở bài tập Sinh học 9
- Chuyên đề Sinh học 9
- Giải bài tập Địa Lí 9
- Giải bài tập Địa Lí 9 (ngắn nhất)
- Giải sách bài tập Địa Lí 9
- Giải Tập bản đồ và bài tập thực hành Địa Lí 9
- Giải bài tập Tiếng anh 9
- Giải sách bài tập Tiếng Anh 9
- Giải bài tập Tiếng anh 9 thí điểm
- Giải sách bài tập Tiếng Anh 9 mới
- Giải bài tập Lịch sử 9
- Giải bài tập Lịch sử 9 (ngắn nhất)
- Giải tập bản đồ Lịch sử 9
- Giải Vở bài tập Lịch sử 9
- Giải bài tập GDCD 9
- Giải bài tập GDCD 9 (ngắn nhất)
- Giải sách bài tập GDCD 9
- Giải bài tập Tin học 9
- Giải bài tập Công nghệ 9

Trang web chia sẻ nội dung miễn phí dành cho người Việt.
Lớp 3Lớp 4Lớp 5Lớp 6Lớp 7Lớp 8Lớp 9Lớp 10Lớp 11Lớp 12Lập trìnhTiếng Anh
Liên hệ với chúng tôi
Ngõ 18 Tả Thanh Oai, Thanh Trì, Hà Nội
Phone: 01689933602
Email: vietjackteam@gmail.com


2015 © All Rights Reserved.
Tuyển dụng
Về chúng tôi
-
-
Ôn tập chương I
Bài 70 (trang 40 SGK Toán 9 Tập 1): Tìm giá trị các biểu thức sau bằng cách biến đổi, rút gọn thích hợp:
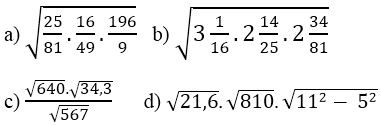
Lời giải:


Tham khảo lời giải các bài tập Toán 9 bài ôn tập chương I khác:
Câu hỏi ôn tập Chương 1 (trang 39 SGK Toán 9 Tập 1):1. Nêu điều kiện để x là căn bậc hai ... 2. Chứng minh √a2 = |a| ...
Bài 70 (trang 40 SGK Toán 9 Tập 1):Tìm giá trị các biểu thức sau bằng cách...
Bài 71 (trang 40 SGK Toán 9 Tập 1):Rút gọn các biểu thức sau:...
Bài 72 (trang 40 SGK Toán 9 Tập 1):Phân tích thành nhân tử (với các số...
Bài 73 (trang 40 SGK Toán 9 Tập 1):Rút gọn rồi tính giá trị các biểu thức sau:...
Bài 74 (trang 40 SGK Toán 9 Tập 1):Tìm x, biết:...
Bài 75 (trang 40 SGK Toán 9 Tập 1):Chứng minh các đẳng thức sau:...
Bài 76 (trang 41 SGK Toán 9 Tập 1):Cho biểu thức...
Mục lục Giải bài tập Toán 9 theo chương:
- Tập 1
- Chương I: Căn Bậc Hai. Căn Bậc Ba
- Chương II: Hàm Số Bậc Nhất
- Chương I: Hệ Thức Lượng Trong Tam Giác Vuông
- Chương II: Đường Tròn
- Tập 2
- Chương III: Hệ Hai Phương Trình Bậc Nhất Hai Ẩn
- Chương IV: Hàm Số y = ax2 (a ≠ 0) - Phương Trình Bậc Hai Một Ẩn
- Chương III: Góc Với Đường Tròn
- Chương IV: Hình Trụ - Hình Nón - Hình Cầu
Đã có app VietJack trên điện thoại, giải bài tập SGK, soạn văn, văn mẫu.... Tải App để chúng tôi phục vụ tốt hơn.
Tải App cho Android hoặc Tải App cho iPhone
Loạt bài Giải bài tập Toán lớp 9 | Để học tốt Toán 9 của chúng tôi được biên soạn bám sát theo chương trình Sách giáo khoa Toán 9 (Tập 1 & Tập 2) và một phần dựa trên quyển sách Giải bài tập Toán 9 và Để học tốt Toán lớp 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
Trang trước
Trang sau
Các loạt bài lớp 9 khác
- Soạn Văn 9
- Soạn Văn 9 (bản ngắn nhất)
- Văn mẫu lớp 9
- Đề kiểm tra Ngữ Văn 9 (có đáp án)
- Giải bài tập Toán 9
- Giải sách bài tập Toán 9
- Đề kiểm tra Toán 9
- Đề thi vào 10 môn Toán
- Chuyên đề Toán 9
- Giải bài tập Vật lý 9
- Giải sách bài tập Vật Lí 9
- Giải bài tập Hóa học 9
- Chuyên đề: Lý thuyết - Bài tập Hóa học 9 (có đáp án)
- Giải bài tập Sinh học 9
- Giải Vở bài tập Sinh học 9
- Chuyên đề Sinh học 9
- Giải bài tập Địa Lí 9
- Giải bài tập Địa Lí 9 (ngắn nhất)
- Giải sách bài tập Địa Lí 9
- Giải Tập bản đồ và bài tập thực hành Địa Lí 9
- Giải bài tập Tiếng anh 9
- Giải sách bài tập Tiếng Anh 9
- Giải bài tập Tiếng anh 9 thí điểm
- Giải sách bài tập Tiếng Anh 9 mới
- Giải bài tập Lịch sử 9
- Giải bài tập Lịch sử 9 (ngắn nhất)
- Giải tập bản đồ Lịch sử 9
- Giải Vở bài tập Lịch sử 9
- Giải bài tập GDCD 9
- Giải bài tập GDCD 9 (ngắn nhất)
- Giải sách bài tập GDCD 9
- Giải bài tập Tin học 9
- Giải bài tập Công nghệ 9

Trang web chia sẻ nội dung miễn phí dành cho người Việt.
Lớp 3Lớp 4Lớp 5Lớp 6Lớp 7Lớp 8Lớp 9Lớp 10Lớp 11Lớp 12Lập trìnhTiếng Anh
Liên hệ với chúng tôi
Ngõ 18 Tả Thanh Oai, Thanh Trì, Hà Nội
Phone: 01689933602
Email: vietjackteam@gmail.com


2015 © All Rights Reserved.
Tuyển dụng
Về chúng tôi
-
-
Bài 71 (trang 40 SGK Toán 9 Tập 1): Rút gọn các biểu thức sau:
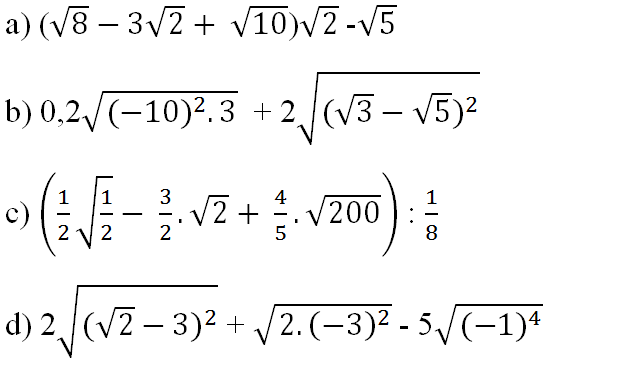
Lời giải:

= (2√2 - 3√2 + 10)√2 - √5
= 2.(√2)2 - 3.(√2)2 + √10.√2 - √5
= 4 - 6 + √20 - √5 = -2 + 2√5 - √5
= -2 + √5
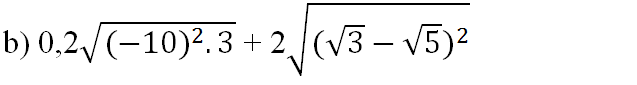
= 0,2.10.√3 + 2|√3 - √5|
s
= 2√3 + 2(√5 - √3)
= 2√3 + 2√5 - 2√3 = 2√5
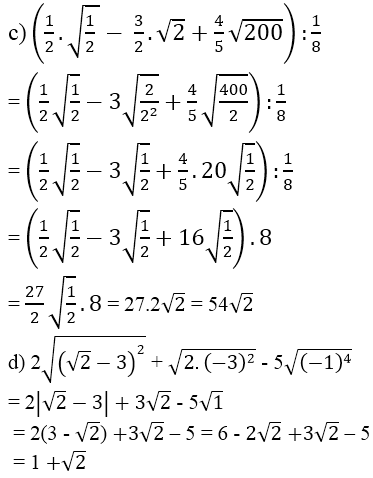
Tham khảo lời giải các bài tập Toán 9 bài ôn tập chương I khác:
Câu hỏi ôn tập Chương 1 (trang 39 SGK Toán 9 Tập 1):1. Nêu điều kiện để x là căn bậc hai ... 2. Chứng minh √a2 = |a| ...
Bài 70 (trang 40 SGK Toán 9 Tập 1):Tìm giá trị các biểu thức sau bằng cách...
Bài 71 (trang 40 SGK Toán 9 Tập 1):Rút gọn các biểu thức sau:...
Bài 72 (trang 40 SGK Toán 9 Tập 1):Phân tích thành nhân tử (với các số...
Bài 73 (trang 40 SGK Toán 9 Tập 1):Rút gọn rồi tính giá trị các biểu thức sau:...
Bài 74 (trang 40 SGK Toán 9 Tập 1):Tìm x, biết:...
Bài 75 (trang 40 SGK Toán 9 Tập 1):Chứng minh các đẳng thức sau:...
Bài 76 (trang 41 SGK Toán 9 Tập 1):Cho biểu thức...
Mục lục Giải bài tập Toán 9 theo chương:
- Tập 1
- Chương I: Căn Bậc Hai. Căn Bậc Ba
- Chương II: Hàm Số Bậc Nhất
- Chương I: Hệ Thức Lượng Trong Tam Giác Vuông
- Chương II: Đường Tròn
- Tập 2
- Chương III: Hệ Hai Phương Trình Bậc Nhất Hai Ẩn
- Chương IV: Hàm Số y = ax2 (a ≠ 0) - Phương Trình Bậc Hai Một Ẩn
- Chương III: Góc Với Đường Tròn
- Chương IV: Hình Trụ - Hình Nón - Hình Cầu
Đã có app VietJack trên điện thoại, giải bài tập SGK, soạn văn, văn mẫu.... Tải App để chúng tôi phục vụ tốt hơn.
Tải App cho Android hoặc Tải App cho iPhone
Loạt bài Giải bài tập Toán lớp 9 | Để học tốt Toán 9 của chúng tôi được biên soạn bám sát theo chương trình Sách giáo khoa Toán 9 (Tập 1 & Tập 2) và một phần dựa trên quyển sách Giải bài tập Toán 9 và Để học tốt Toán lớp 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
Trang trước
Trang sau
Các loạt bài lớp 9 khác
- Soạn Văn 9
- Soạn Văn 9 (bản ngắn nhất)
- Văn mẫu lớp 9
- Đề kiểm tra Ngữ Văn 9 (có đáp án)
- Giải bài tập Toán 9
- Giải sách bài tập Toán 9
- Đề kiểm tra Toán 9
- Đề thi vào 10 môn Toán
- Chuyên đề Toán 9
- Giải bài tập Vật lý 9
- Giải sách bài tập Vật Lí 9
- Giải bài tập Hóa học 9
- Chuyên đề: Lý thuyết - Bài tập Hóa học 9 (có đáp án)
- Giải bài tập Sinh học 9
- Giải Vở bài tập Sinh học 9
- Chuyên đề Sinh học 9
- Giải bài tập Địa Lí 9
- Giải bài tập Địa Lí 9 (ngắn nhất)
- Giải sách bài tập Địa Lí 9
- Giải Tập bản đồ và bài tập thực hành Địa Lí 9
- Giải bài tập Tiếng anh 9
- Giải sách bài tập Tiếng Anh 9
- Giải bài tập Tiếng anh 9 thí điểm
- Giải sách bài tập Tiếng Anh 9 mới
- Giải bài tập Lịch sử 9
- Giải bài tập Lịch sử 9 (ngắn nhất)
- Giải tập bản đồ Lịch sử 9
- Giải Vở bài tập Lịch sử 9
- Giải bài tập GDCD 9
- Giải bài tập GDCD 9 (ngắn nhất)
- Giải sách bài tập GDCD 9
- Giải bài tập Tin học 9
- Giải bài tập Công nghệ 9

Trang web chia sẻ nội dung miễn phí dành cho người Việt.
Lớp 3Lớp 4Lớp 5Lớp 6Lớp 7Lớp 8Lớp 9Lớp 10Lớp 11Lớp 12Lập trìnhTiếng Anh
Liên hệ với chúng tôi
Ngõ 18 Tả Thanh Oai, Thanh Trì, Hà Nội
Phone: 01689933602
Email: vietjackteam@gmail.com


2015 © All Rights Reserved.
Tuyển dụng
Về chúng tôi
-
-
-

ài 72 (trang 40 SGK Toán 9 Tập 1): Phân tích thành nhân tử (với các số x, y, a, b không âm và a ≥ b)
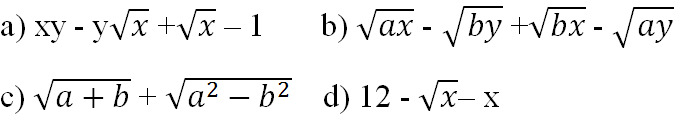
Lời giải:
a) xy - y√x + √x - 1
= (√x)2.y - y√x + √x - 1
= y√x(√x - 1) + √x - 1
= (√x - 1)(y√x + 1) với x ≥ 1
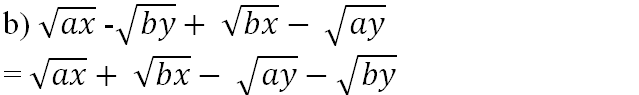
= √x(√a + √b) - √y(√a + √b)
= (√a + √b)(√x - √y) (với x, y, a và b đều không âm)
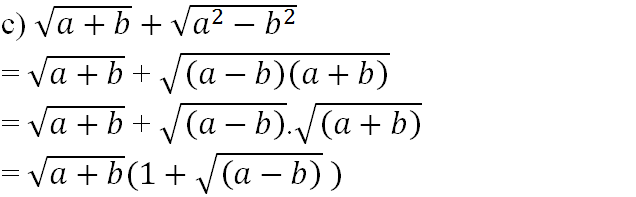
(với a + b, a - b đều không âm)
d) 12 - √x - x
= 16 - x - 4 - √x (tách 12 = 16 - 4 và đổi vị trí)
= [42 - (√x)2] - (4 + √x)
= (4 - √x)(4 + √x) - (4 + √x)
= (4 + √x)(4 - √x - 1)
= (4 + √x)(3 - √x)
Tham khảo lời giải các bài tập Toán 9 bài ôn tập chương I khác:
Câu hỏi ôn tập Chương 1 (trang 39 SGK Toán 9 Tập 1):1. Nêu điều kiện để x là căn bậc hai ... 2. Chứng minh √a2 = |a| ...
Bài 70 (trang 40 SGK Toán 9 Tập 1):Tìm giá trị các biểu thức sau bằng cách...
Bài 71 (trang 40 SGK Toán 9 Tập 1):Rút gọn các biểu thức sau:...
Bài 72 (trang 40 SGK Toán 9 Tập 1):Phân tích thành nhân tử (với các số...
Bài 73 (trang 40 SGK Toán 9 Tập 1):Rút gọn rồi tính giá trị các biểu thức sau:...
Bài 74 (trang 40 SGK Toán 9 Tập 1):Tìm x, biết:...
Bài 75 (trang 40 SGK Toán 9 Tập 1):Chứng minh các đẳng thức sau:...
Bài 76 (trang 41 SGK Toán 9 Tập 1):Cho biểu thức...
Mục lục Giải bài tập Toán 9 theo chương:
- Tập 1
- Chương I: Căn Bậc Hai. Căn Bậc Ba
- Chương II: Hàm Số Bậc Nhất
- Chương I: Hệ Thức Lượng Trong Tam Giác Vuông
- Chương II: Đường Tròn
- Tập 2
- Chương III: Hệ Hai Phương Trình Bậc Nhất Hai Ẩn
- Chương IV: Hàm Số y = ax2 (a ≠ 0) - Phương Trình Bậc Hai Một Ẩn
- Chương III: Góc Với Đường Tròn
- Chương IV: Hình Trụ - Hình Nón - Hình Cầu
Đã có app VietJack trên điện thoại, giải bài tập SGK, soạn văn, văn mẫu.... Tải App để chúng tôi phục vụ tốt hơn.
Tải App cho Android hoặc Tải App cho iPhone
Loạt bài Giải bài tập Toán lớp 9 | Để học tốt Toán 9 của chúng tôi được biên soạn bám sát theo chương trình Sách giáo khoa Toán 9 (Tập 1 & Tập 2) và một phần dựa trên quyển sách Giải bài tập Toán 9 và Để học tốt Toán lớp 9.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các bình luận không phù hợp với nội quy bình luận trang web sẽ bị cấm bình luận vĩnh viễn.
Trang trước
Trang sau
Các loạt bài lớp 9 khác
- Soạn Văn 9
- Soạn Văn 9 (bản ngắn nhất)
- Văn mẫu lớp 9
- Đề kiểm tra Ngữ Văn 9 (có đáp án)
- Giải bài tập Toán 9
- Giải sách bài tập Toán 9
- Đề kiểm tra Toán 9
- Đề thi vào 10 môn Toán
- Chuyên đề Toán 9
- Giải bài tập Vật lý 9
- Giải sách bài tập Vật Lí 9
- Giải bài tập Hóa học 9
- Chuyên đề: Lý thuyết - Bài tập Hóa học 9 (có đáp án)
- Giải bài tập Sinh học 9
- Giải Vở bài tập Sinh học 9
- Chuyên đề Sinh học 9
- Giải bài tập Địa Lí 9
- Giải bài tập Địa Lí 9 (ngắn nhất)
- Giải sách bài tập Địa Lí 9
- Giải Tập bản đồ và bài tập thực hành Địa Lí 9
- Giải bài tập Tiếng anh 9
- Giải sách bài tập Tiếng Anh 9
- Giải bài tập Tiếng anh 9 thí điểm
- Giải sách bài tập Tiếng Anh 9 mới
- Giải bài tập Lịch sử 9
- Giải bài tập Lịch sử 9 (ngắn nhất)
- Giải tập bản đồ Lịch sử 9
- Giải Vở bài tập Lịch sử 9
- Giải bài tập GDCD 9
- Giải bài tập GDCD 9 (ngắn nhất)
- Giải sách bài tập GDCD 9
- Giải bài tập Tin học 9
- Giải bài tập Công nghệ 9

Trang web chia sẻ nội dung miễn phí dành cho người Việt.
Lớp 3Lớp 4Lớp 5Lớp 6Lớp 7Lớp 8Lớp 9Lớp 10Lớp 11Lớp 12Lập trìnhTiếng Anh
Liên hệ với chúng tôi
Ngõ 18 Tả Thanh Oai, Thanh Trì, Hà Nội
Phone: 01689933602
Email: vietjackteam@gmail.com


2015 © All Rights Reserved.
Tuyển dụng
Về chúng tôi
hihihihhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh






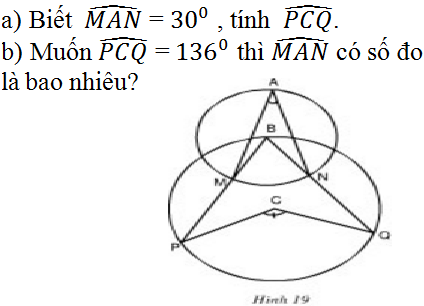
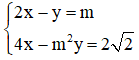

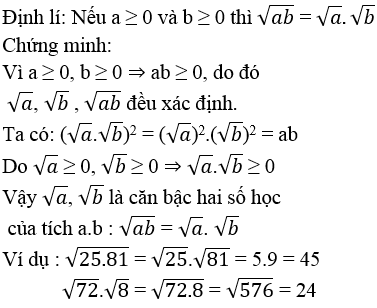
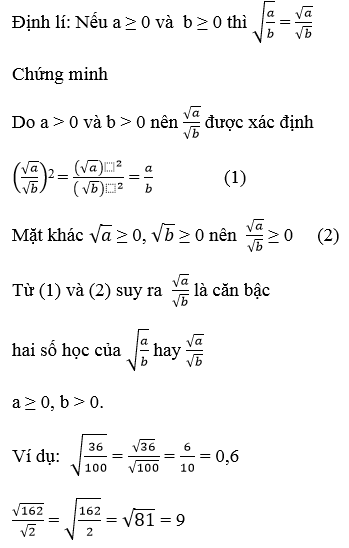

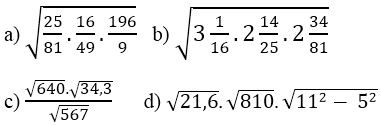


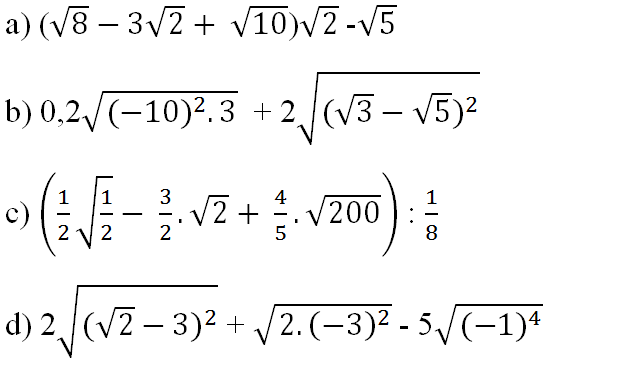

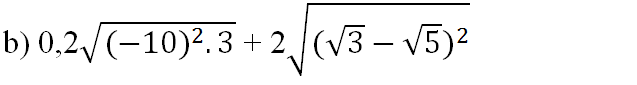
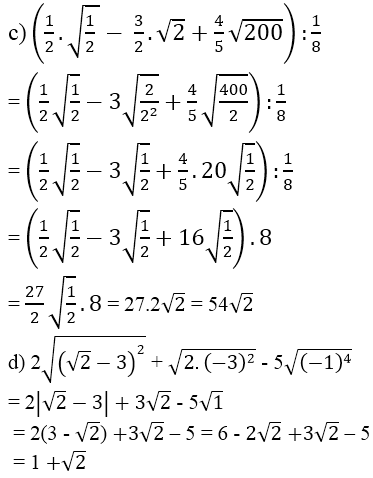
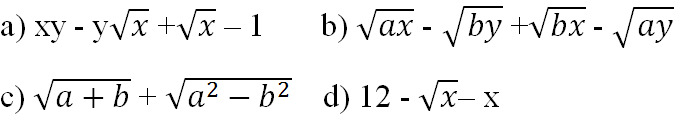
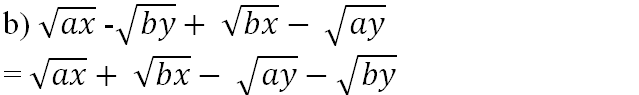
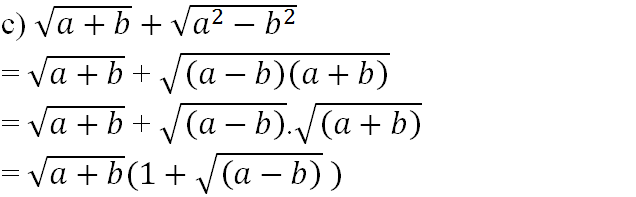
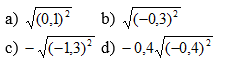
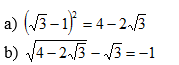
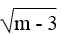 )x + 2/3
)x + 2/3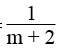 t - 3/4 (t là biến số)
t - 3/4 (t là biến số)
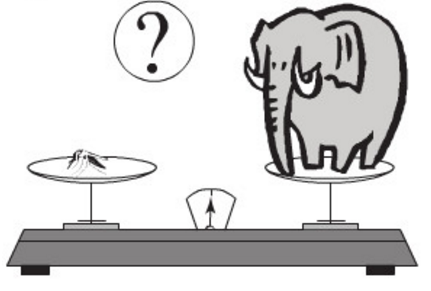
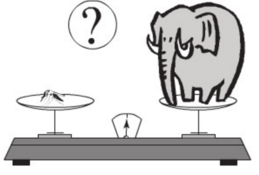
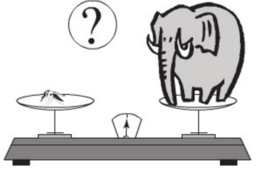
Sai lầm ở chỗ: sau khi lấy căn hai vế của (m – V)2 = (V – m)2 ta phải được kết quả |m – V| = |V – m| chứ không thể có m – V = V – m (theo hằng đẳng thức √A2 = |A|.
Do đó, con muỗi không thể nặng bằng con voi.
sai o cho sau khi lay can 2 ve cua (m-V)\(^2\)
=(V-m)\(^2\) ta dc ket qua \(|m-V|=|V-m|\)
Do do con muoi ko the nang bang con voi