Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
e/
\(\left\{{}\begin{matrix}\Delta'=\left(m-1\right)^2-4\left(m-1\right)>0\\x_1+x_2=\frac{1-m}{2}>0\\x_1x_2=\frac{m-1}{4}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(m-5\right)>0\\m< 1\\m>1\end{matrix}\right.\)
Không tồn tại m thỏa mãn
f/
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(m-2\right)^2-\left(m-2\right)>0\\x_1+x_2=2>0\\x_1x_2=\frac{1}{m-2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\\left(m-2\right)\left(m-3\right)>0\\m-2>0\end{matrix}\right.\)
\(\Rightarrow m>3\)
c/
\(\left\{{}\begin{matrix}\Delta=\left(m-2\right)^2-4\left(m+1\right)>0\\x_1+x_2=2-m>0\\x_1x_2=m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-8m>0\\m< 2\\m>-1\end{matrix}\right.\)
\(\Rightarrow-1< m< 0\)
d/
\(\left\{{}\begin{matrix}\Delta=\left(m-3\right)^2+4\left(m+1\right)>0\\x_1+x_2=3-m>0\\x_1x_2=-m-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-2m+13>0\\m< 3\\m< -1\end{matrix}\right.\)
\(\Rightarrow m< -1\)
Để pt có 2 nghiệm dương (ko yêu cầu pb?) \(\left\{{}\begin{matrix}a\ne0\\\Delta\ge0\\x_1+x_2=-\frac{b}{a}>0\\x_1x_2=\frac{c}{a}>0\end{matrix}\right.\)
a/ \(\left\{{}\begin{matrix}\Delta=\left(2m-1\right)^2+4m-4\ge0\\x_1+x_2=2m+1>0\\x_1x_2=-m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-3\ge0\\m>-\frac{1}{2}\\m< 1\end{matrix}\right.\) \(\Rightarrow\frac{\sqrt{3}}{2}\le m< 1\)
b/ \(\left\{{}\begin{matrix}\Delta=\left(m+2\right)^2-4\left(-2m+1\right)\ge0\\-m-2>0\\-2m+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+12m\ge0\\m< -2\\m< \frac{1}{2}\end{matrix}\right.\) \(\Rightarrow m\le-12\)
e/
\(\left\{{}\begin{matrix}\Delta=\left(m+1\right)^2-4m\ge0\\x_1+x_2=m+1>0\\x_1x_2=m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2\ge0\\m>-1\\m>0\end{matrix}\right.\) \(\Rightarrow m>0\)
f/
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)\ge0\\x_1+x_2=\frac{2\left(3-2m\right)}{m-2}>0\\x_1x_2=\frac{5m-6}{m-2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3\ge0\\\frac{3-2m}{m-2}>0\\\frac{5m-6}{m-2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1\le m\le3\\\frac{3}{2}< m< 2\\\left[{}\begin{matrix}m< \frac{6}{5}\\m>2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
e/
\(\left\{{}\begin{matrix}\Delta=\left(m+1\right)^2-4\left(m-1\right)\ge0\\x_1+x_2=m+1< 0\\x_1x_2=m-1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-2m+5>0\\m< -1\\m>1\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
f/
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(m-2\right)^2-\left(m-2\right)\ge0\\x_1+x_2=2< 0\left(vô-lý\right)\\x_1x_2=\frac{1}{m-2}>0\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
c/
\(\left\{{}\begin{matrix}\Delta=m^2-4\left(m-\frac{3}{4}\right)\ge0\\x_1+x_2=-m< 0\\x_1x_2=m-\frac{3}{4}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-4m+3\ge0\\m>0\\m>\frac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\ge3\\\frac{3}{4}< m\le1\end{matrix}\right.\)
d/
\(\left\{{}\begin{matrix}\Delta'=4\left(2m-1\right)^2-4m\ge0\\x_1+x_2=1-2m< 0\\x_1x_2=\frac{m}{4}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2-5m+1\ge0\\m>\frac{1}{2}\\m>0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
\(\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=m+1-1=m\\x_2=m+1+1=m+2\end{matrix}\right.\)
\(\left|x_1\right|=3\left|x_2\right|\Leftrightarrow\left|m\right|=3\left|m+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3m+6=-m\\3m+6=m\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-3\end{matrix}\right.\)
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0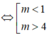 
Do x1 < x2 < 1
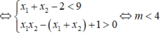
a.
Pt có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+3\right)^2-\left(m+1\right)\left(-m+2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\2m^2+7m+7>0\left(\text{luôn đúng}\right)\end{matrix}\right.\)
\(\Rightarrow m\ne-1\)
b.
BPT vô nghiệm khi \(\left(m^2-4m-5\right)x^2+2\left(m-5\right)-1< 0\) nghiệm đúng với mọi x
- Với \(m=-1\) ko thỏa mãn
- Với \(m=5\) thỏa mãn
- Với \(m\ne\left\{-1;5\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-4m-5< 0\\\Delta'=\left(m-5\right)^2+m^2-4m-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\\left(m-5\right)\left(2m-4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1< m< 5\\2< m< 5\end{matrix}\right.\) \(\Rightarrow2< m< 5\)
Kết hợp lại ta được: \(2< m\le5\)
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
( m 2 + m + 3 ) x 2 + ( 4 m 2 + m + 2 ) x + m = 0 có a = m 2 + m + 3 > 0, ∀m và có b = 4 m 2 + m + 2 > 0, ∀m, nên ab > 0, ∀m. Vì vậy không có giá trị nào của m để phương trình đã cho có hai nghiệm dương phân biệt.
dương phân biệt á bạn ơi
Phương trình có hai nghiệm âm phân biệt hay dương phân biệt bạn?
Hay hai nghiệm trái dấu?