Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(Đpcm)
b) Ta có: ΔBAD=ΔBED(cmt)
nên AD=ED(hai cạnh tương ứng)
Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADK=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: AK=EC(hai cạnh tương ứng)
c) Ta có: BA+AK=BK(A nằm giữa B và K)
BE+EC=BC(E nằm giữa B và C)
mà BA=BE(cmt)
và AK=EC(cmt)
nên BK=BC
Ta có: ΔADK=ΔEDC(cmt)
nên DK=DC(hai cạnh tương ứng)
Ta có: M là trung điểm của CK(cmt)
nên MK=MC
Ta có: BK=BC(cmt)
nên B nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DK=DC(cmt)
nên D nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: CM=KM(cmt)
nên M nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(3)
Từ (1), (2) và (3) suy ra B,D,M thẳng hàng(đpcm)

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

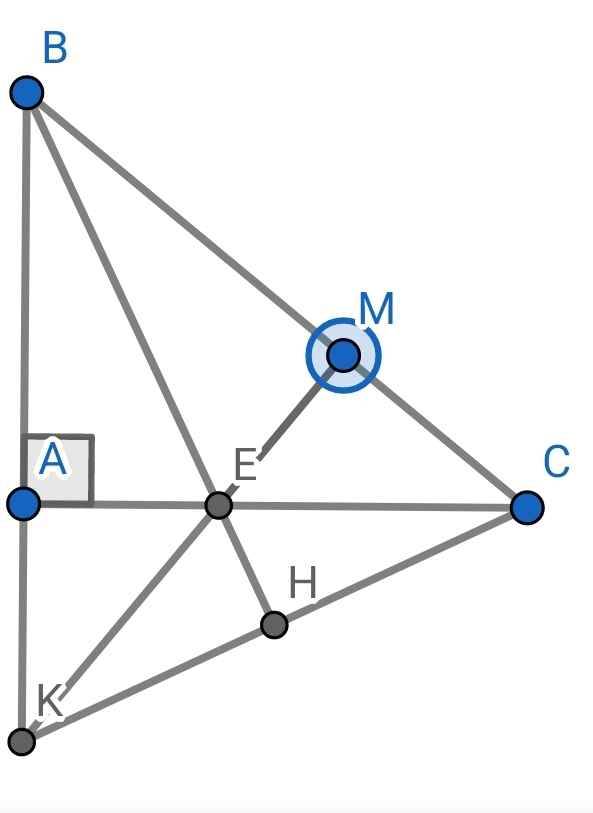
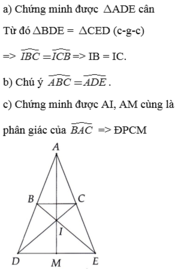
a) Xét ∆ABE và ∆MBE có:
BE chung
góc ABE = góc MBE (BE là phân giác của góc ABC)
AB = BM
⇒∆ABE = ∆MBE (c-g-c)
⇒góc BAE = góc BME (hai góc tương ứng)
⇒ME vuông góc BC
b) Do ∆ABE = ∆MBE (cmt)
⇒AE = ME (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆AEK và ∆MEC có:
AE = ME (cmt)
góc AEK = góc MEC (đối đỉnh)
⇒∆AEK = ∆MEC (cạnh góc vuông - góc nhọn kề)
⇒EK = EC (hai cạnh tương ứng)
AK = MC (hai cạnh tương ứng)
Lại có: BK = BA + AK
BC = BM + MC
⇒BK = BC
c) Gọi H là giao điểm của BE và CK
Xét ∆BHK và ∆BHC có:
BK = BC (cmt)
góc HBK = góc HBC (do BE là tia phân giác của góc ABC)
BH chung
⇒∆BHK = ∆BHC (c-g-c)
⇒góc BHK = góc BHC (hai góc tương ứng)
Mà góc BHK + góc BHC = 180⁰ (kề bù)
⇒góc BHK = góc BHC = 180⁰ : 2 = 90⁰
⇒BH vuông góc KC
Hay BE vuông góc KC

a) Xét ΔABE và ΔMBE có:
BE chung
AB = MB (gt)
AE = EM (E là trung điểm của AM)
Suy ra ΔABE = ΔMBE (ccc)
b) Xét Δ ABK và Δ MBK có:
AB = BM (gt)
góc ABK = góc MBK (ΔABE = ΔMBE)
BK chung
Suy ra ΔABK = ΔMBK (cgc)
Suy ra góc BAK = góc BMK
Mà góc BAK = 90 độ ( ΔABC vuông tại A)
Suy ra góc BMK = 90 độ
Suy ra KM ⊥ BC (đng)
a: Xét ΔABE và ΔMBE co
BA=BM
EA=EM
BE chung
=>ΔABE=ΔMBE
b: Xet ΔBAK và ΔBMK có
BA=BM
góc ABK=góc MBK
BK chung
=>ΔBAK=ΔBMK
=>góc BMK=90 độ
=>KM vuông góc BC
c: Xét tứ giác MFKQ có
MF//KQ
MF=KQ
=>MFKQ là hình bình hành
=>MQ//KF
=>góc CMQ=góc CBK=góc ABK

Giải
a) vì m la trung diểm của BC => BM=MC
Xét tam giac BAM va tam giac MAC có:
AB=AC(dề bài cho)
BM=MC(Chung minh tren)
AM la cạnh chung(de bai cho)
=>Tam giác BAM=tam giac MAC(c.c.c)
b)từ trên
=>góc BAM=góc MAC(hai goc tuong ung)
Tia AM nam giua goc BAC (1)
goc BAM=goc MAC(2)
từ (1) va (2)
=>AM la tia phan giac cua goc BAC
c)Còn nữa ......-->

a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)
Suy ra: BA=BH(hai cạnh tương ứng) và EA=EH(hai cạnh tương ứng)
Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH(cmt)
\(\widehat{AEK}=\widehat{HEC}\)(hai góc đối đỉnh)
Do đó: ΔAEK=ΔHEC(Cạnh góc vuông-góc nhọn kề)
Suy ra: EK=EC(hai cạnh tương ứng) và AK=HC(Hai cạnh tương ứng)
Ta có: BK=BA+AK
BC=BH+HC
mà BA=BH(cmt)
và AK=HC(cmt)
nên BK=BC
Ta có: BK=BC(cmt)
nên B nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EK=EC(cmt)
nên E nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của KC
hay BE\(\perp\)KC
b) Ta có: EA=EH(cmt)
mà EH<EC
nên EA<EC