Question

[Yumi]

Bài 1 (trang 105 SGK Đại Số 10): Xét dấu các tam thức bậc hai:

a) 5x2 - 3x + 1 ;      b) -2x2 + 3x + 5

c) x2 + 12x + 36 ;      d) (2x - 3)(x + 5)

Các bạn giúp mình với

Answer 1

[KAl(SO4)2·12H2O]

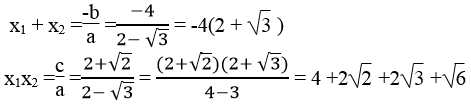
a) \(f\left(x\right)=5x^2-3x+1\text{ có }\Delta=9-20=-11< 0\text{ và có Hsố là: }a=5>0\text{ nên }f\left(x\right)>0;\forall x\inℝ\)

b) \(f\left(x\right)=-2x^2+3x+5\text{ có }\Delta=9+40=49\)

Tam thức có hai nghiệm phân biệt: \(\orbr{\begin{cases}x_1=-1\\x_2=\frac{5}{2}\end{cases}}\)

Ta có bảng xét dấu:

x f(x) -∞ -1 5/2 +∞ - 0 + 0 -

\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left\{-1;\frac{5}{2}\right\}\)

    \(f\left(x\right)=0\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{5}{2}\end{cases}}\)

  \(f\left(x\right)< 0\Leftrightarrow x\in\left\{-\infty;-1\right\}\text{∪}\left\{\frac{5}{2};+\infty\right\}\)

c) \(f\left(x\right)=x^2+12x+36\text{ có }\Delta=0\Rightarrow\text{Nghiệm là: }-6\)

Ta có bảng xét dấu:

x f(x) -∞ -6 +∞ + 0 +

\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\ne-6\)

    \(f\left(x\right)=0\Leftrightarrow x=-6\)

Ta có thể phân tích như sau: \(f\left(x\right)=\left(x+6\right)^2\ge0;\forall x\inℝ\)

d) \(f\left(x\right)=\left(2x-3\right)\left(x+5\right)\text{ có hai nghiệm phân biệt: }\orbr{\begin{cases}x_1=\frac{3}{2}\\x_2=-5\end{cases}}\)

Ta có bảng xét dấu: 

x -∞ -5 3/2 +∞ f(x) + 0 - 0 +

\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left\{-\infty;-5\right\}\text{∪}\left\{\frac{3}{2};+\infty\right\}\)

    \(f\left(x\right)=0\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{3}{2}\end{cases}}\)

  \(f\left(x\right)< 0\Leftrightarrow x\in\left\{-5;\frac{3}{2}\right\}\)