Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(\dfrac{1}{11}>\dfrac{1}{20}\\ \dfrac{1}{12}>\dfrac{1}{20}\\ ..........\\ \dfrac{1}{20}=\dfrac{1}{20}\)
\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\\ \Rightarrow S>\dfrac{10}{20}\\ \Rightarrow S>\dfrac{1}{2}\)

a: 17/200>17/314
b: 11/54=22/108<22/37
c: 141/893=3/19
159/901=3/17
mà 3/19<3/17
nên 141/893<159/901

a) \(\dfrac{-1}{-4}\)=\(\dfrac{1}{4}>0\)
\(\dfrac{3}{-4}< 0\)
\(\Rightarrow\dfrac{1}{4}>\dfrac{3}{-4}hay\dfrac{-1}{-4}>\dfrac{3}{-4}\)
b) Ta có:
\(\dfrac{15}{17}=1-\dfrac{2}{17}\\ \)
\(\dfrac{25}{27}=1-\dfrac{2}{27}\\ \\ \)
Mà \(\dfrac{2}{17}>\dfrac{2}{27}\left(17< 27\right)\)
\(\Rightarrow1-\dfrac{2}{17}< 1-\dfrac{2}{27}\)hay \(\dfrac{15}{17}< \dfrac{25}{27}\)

a) \(\dfrac{3}{4}+\dfrac{3}{5}-\dfrac{18}{60}\) ( MTC: 60)
= \(\dfrac{3.15}{4.15}+\dfrac{3.12}{5.12}-\dfrac{18}{60}\)
= \(\dfrac{45}{60}+\dfrac{36}{60}-\dfrac{18}{60}\)
= \(\dfrac{45+36-18}{60}\)=\(\dfrac{63}{60}=\dfrac{21}{20}\)
b)\(\dfrac{17}{8}-\dfrac{11}{6}-\dfrac{2}{9}\) (MTC:72)
=\(\dfrac{17.9}{8.9}-\dfrac{11.12}{6.12}-\dfrac{2.8}{9.8}\)
= \(\dfrac{153}{72}-\dfrac{132}{72}-\dfrac{16}{72}\)
=\(\dfrac{153-132-16}{72}\)
=\(\dfrac{5}{72}\)
c)\(\dfrac{23}{29}+\dfrac{5}{11}+\dfrac{17}{11}\) (MTC:319)
= \(\dfrac{23.11}{29.11}+\dfrac{5.29}{11.29}+\dfrac{17.29}{11.29}\)
=\(\dfrac{253}{319}+\dfrac{145}{319}+\dfrac{493}{319}\)
=\(\dfrac{253+145+493}{319}\)=\(\dfrac{891}{319}=\dfrac{81}{29}\)
c) \(\dfrac{20}{45}+\dfrac{14}{35}+\dfrac{32}{44}\)
= \(\dfrac{4}{9}+\dfrac{2}{5}+\dfrac{8}{11}\)(Rút gọn b/thức)(MTC:495)
=\(\dfrac{4.55}{9.55}+\dfrac{2.99}{5.99}+\dfrac{8.45}{11.45}\)
=\(\dfrac{220}{495}+\dfrac{198}{495}+\dfrac{360}{495}\)
=\(\dfrac{220+198+360}{495}\)=\(\dfrac{778}{495}\)
e)\(17\dfrac{25}{27}+3\dfrac{7}{2}\)
= \(\dfrac{484}{27}+\dfrac{13}{2}\) (MTC:54)
=\(\dfrac{484.2}{27.2}+\dfrac{13.27}{2.27}\)
\(=\dfrac{968}{54}+\dfrac{351}{54}\)
=\(\dfrac{968+351}{54}=\dfrac{1319}{54}\)

tính chất trên gọi là tính chất bắc cầu, ta so sánh hai phân số với một số (phân số) thứ 3.

a: 14/21=2/3=4/6
60/72=5/6
mà 4<5
nên 14/21<60/72
b: 38/133=2/7=16/56
129/344=3/8=21/56
mà 16<21
nên 38/133<129/344

Ta có: \(\dfrac{1}{11}>\dfrac{1}{20}\)
\(\dfrac{1}{12}>\dfrac{1}{20}\)
\(\dfrac{1}{13}>\dfrac{1}{20}\)
\(\dfrac{1}{14}>\dfrac{1}{20}\)
\(\dfrac{1}{15}>\dfrac{1}{20}\)
\(\dfrac{1}{16}>\dfrac{1}{20}\)
\(\dfrac{1}{17}>\dfrac{1}{20}\)
\(\dfrac{1}{18}>\dfrac{1}{20}\)
\(\dfrac{1}{19}>\dfrac{1}{20}\)
\(\dfrac{1}{20}=\dfrac{1}{20}\)
=> \(\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{20}>\dfrac{1}{20}.10\)
hay S > \(\dfrac{1}{2}\)
Ta có :
\(\dfrac{1}{11}>\dfrac{1}{20}\) ( vì 1 > 0 , 0 < 11 < 20 )
\(\dfrac{1}{12}>\dfrac{1}{20}\) ( vì 1 > 0 , 0 < 12 < 20 )
...
\(\dfrac{1}{20}=\dfrac{1}{20}\)
\(\Rightarrow\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{20}>\dfrac{1}{20}+\dfrac{1}{20}+...+\dfrac{1}{20}\)( 10 số hạng )
\(\Rightarrow S>\dfrac{1}{20}.10\Rightarrow S>\dfrac{10}{20}\Rightarrow S>\dfrac{1}{2}\)
Vậy ...
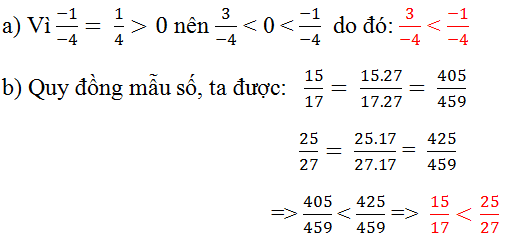
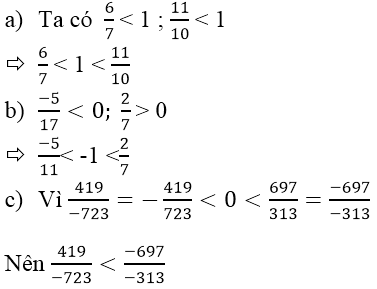
`17/20 = 119/140`
`11/14=110/140`
`=> 119/140 > 110/140`
`=> 17/20 > 11/14`
\(\dfrac{17}{20}=\dfrac{17\cdot14}{20\cdot14}=\dfrac{238}{280}\)
\(\dfrac{11}{14}=\dfrac{11\cdot20}{14\cdot20}=\dfrac{220}{280}\)
mà 238>220
nên \(\dfrac{17}{20}>\dfrac{11}{14}\)