Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.
a)MD vuông góc với AB --> ^MDA=90 độ
ME vuông góc với AC --> ^MEA=90 độ
Mà ^DAE=90 độ => ADME là hình chữ nhật
Tam giác BDM vuông có ^DMB = 45 độ
=> DM=DB
=>Pdme= 2(DM+DA)=2(DB+DA)=2AB=2AC=8(cm)
b) Gọi M' là chân đường cao hạ từ A xuống BC
Ta có: DE=AM ( ADME là hình chữ nhật)
Mà AM≥AM' (Theo tính chất đường xiên)
=> DEmin khi M là chân đường cao hạ từ A xuống BC
Xét tam giác ABC có: \(AC + CB > AB\).
Vậy nên bạn Hoa đi đường thứ nhất đi từ A đến C và đi tiếp từ C đến B sẽ dài hơn đi đường thứ hai đi từ B đến A.
và 
. Hơn nữa, tốc độ bơi trung bình của người đó là 1m/s và tốc độ chạy trung bình là 3m/s. Hỏi:
Vì đường thẳng AB cắt 2 đường thẳng a và b ,trong các góc tạo thánh có một cặp góc đọng vị bằng nhau thì a và b song song với nhau
Kẻ 1 dường thẳng khác và vuông góc với 2 đường thẳng đã cho => 2 đoạn thẳng đó song song
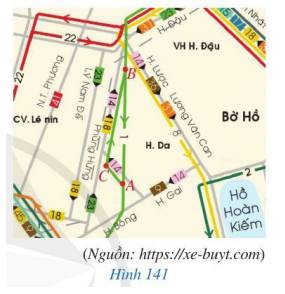
*Có góc ACD là góc ngoài của tam giác DCE nên góc ACD>góc E
Hay BD>CD(1)
*Có góc ABD là góc ngoài của tam giác BCD nên góc ABD>Góc ACD
Hay AD>BD(2)
Từ (1)&(2) ta có AD>BD>CD hay ban C đến B trước bạn A Và Ban B
Chúc bạn học tốt😊😊😊