Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Chu vi là 69,08cm
Độ dài bán kính là 69,08:2:3,14=11(cm)
Sxq=11^2*4*3,14=1519,76cm2
V=4/3*pi*11^3=5572,45cm3

Gọi chiều dài và chiều rộng của sân bóng lần lượt là \(x,y\left(m\right);x,y>0\).
Vì chu vi là \(140m\)nên \(2\left(x+y\right)=140\Leftrightarrow x+y=70\)
Vì giảm chiều rộng đi \(5m\)tăng chiều dài thêm \(8m\)thì diện tích sân bóng không đổi nên
\(\left(x+8\right)\left(y-5\right)=xy\Leftrightarrow-5x+8y=40\)
Ta có hệ phương trình:
\(\hept{\begin{cases}x+y=70\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}5x+5y=350\\-5x+8y=40\end{cases}}\Leftrightarrow\hept{\begin{cases}x=40\\y=30\end{cases}}\)(thỏa mãn)
Vậy chiều dài là \(40m\)chiều rộng là \(30m\).

Áp dụng BĐT sau:\(2\left(a^2+b^2\right)\ge\left(a+b\right)^2\) ( dùng BĐT Bunhiacopski mà chứng minh :D )
Ta có:\(\frac{a+b}{a^2+b^2}=\frac{41}{9}\Rightarrow\frac{a^2+b^2}{a+b}=\frac{41}{9}\)
\(\Rightarrow\frac{82}{9}=\frac{2\left(a^2+b^2\right)}{a+b}\ge\frac{\left(a+b\right)^2}{a+b}=a+b\)
\(\Rightarrow a+b\le9\)
Mặt khác:\(41\left(a+b\right)=9\left(a^2+b^2\right);\left(41;9\right)=1\Rightarrow a+b⋮9\Rightarrow a+b=9\)
\(\Rightarrow a^2+b^2=41\)
Ta có hệ:\(\hept{\begin{cases}a+b=9\\a^2+b^2=41\end{cases}}\) giải cái hệ này là ra a,b nha < 3

Gọi chiều dài là a (m), hiều rộng là b(m)
Có a+b=140 : 2=70 (m)
Chiều dài sau khi tăng là a+8 (m)
chiều rộng sai khi giảm là b-5 (m)
Có hệ ptr a+b=70 (1)
(a+8)(b-5)=ab (2)
(2) <=> 8b-5a-40=0
<=>8b-5a=40
(1)<=> a=70-b
=> (2) <=> 8b+5b-350=40
<=>13b=390
<=>b=30(m)
=> a=40(m)
<=>43b=390

vì hình vuông bằng 4 hình có cùng kích thước
\(\Rightarrow\)chu vi hình vuông gấp đôi chu vi hình chữ nhật ( trừ các cạnh trùng nhau. mỗi hình chữ nhật chỉ tiếp giáp với mặt chu vi hình vuông 2 cạnh( 1 chiều dài, 1 chiều rộng)
chu vi hình vuông là:
40\(\times\)2=80(cm)
Đáp số:80cm

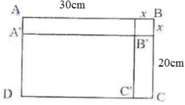
- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)
Khi bớt mỗi kích thước x (cm) thì được một hình chữ nhật có các kích thước
là 20 – x (cm) và 30 – x (cm).
Khi đó chu vi của hình chữ nhật là y=2(20–x+30–x)y=2(20–x+30–x)
hay y=100–4x

- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm.
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm), ta có hình chữ nhật mới là A'B'C'D' có:
A'B' = 30 – x
B'C' = 20 – x
Gọi y là chu vi của hình chữ nhật A'B'C'D', ta có:
y = 2[(30 - x) + (20 - x)]
=> y = 2(50 - 2x)
=> y = -4x + 100 (cm)