Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi vận tốc thực là x (x>2)
=> vxuôi là x+2 (km)
vngược là x-2(km)
ta có pt
5(x+2)=6(x-2)
=> x = 22 (thỏa mãn bài)
=> AB= 22km

Gọi X là vận tốc thức của cano
Khi xuôi dòng ta có: AB= (x+2)4
Khi ngược dòng ta có: AB = (x-2),5
Từ đây ta có pt (x+2)4= (x-2).5
Tìm đc x= 18 vậy S AB= (18+2).4=80 km
Gọi vận tốc thực của ca nô là x km/h thì vận tốc xuôi dòng và ngược dòng của ca nô lần lượt là x + 2 km/h và x - 2 km/h nên khoảng cách từ bến A đến bến B là : 4(x + 2) = 5(x - 2) <=> 4x + 8 = 5x - 10 => 5x = 4x + 8 + 10 = 4x + 18 => 18 = 5x - 4x = x
=> 4(x + 2) = 4.(18 + 2) = 4.20 = 80 hay 5(x - 2) = 5.(18 - 2) = 5.16 = 80. Vậy khoảng cách từ bến A đến bến B là 80 km.

Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.

Vì vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước nên ta có phương trình:
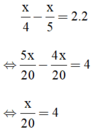
x = 80 (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là 80km.
(Giải thích tại sao hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:
Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:
Khi xuôi dòng: vận tốc canô = v + a
Khi ngược dòng: vận tốc canô = v - a
Hiệu vận tốc = v + a - (v - a) = 2a = 2 vận tốc dòng nước.)

Gọi quãng đường Ab là x (km)
Vận tốc lúc xuôi dòng là: \(\dfrac{x}{4}\) (h)
Vận tốc lúc ngược dòng là: \(\dfrac{x}{5}\)(h)
Theo đề bài ta có PT:
\(\dfrac{x}{4}-\dfrac{x}{5}=2\)
⇔5x-4x=40
⇔x=40
Vậy quãng đường AB dài 40km
Gọi khoảng cách giữa 2 bến a và b là x ( km )
Vận tốc ca nô lúc xuôi dòng là: \(\dfrac{x}{4}\) ( km/h )
Vận tốc ca nô lúc ngược dòng là: \(\dfrac{x}{5}\) ( km/h )
Vì vận tốc xuôi dòng - vận tốc ngược dòng = 2 lần vận tốc dòng nước
⇒ x\(\dfrac{x}{4}-\dfrac{x}{5}=4\)
⇒ \(\dfrac{5x}{20}-\dfrac{4x}{20}=\dfrac{80}{20}\)
⇒ x = 80
Vậy: Khoảng cách giữa 2 bến a và b là 80 km.

Gọi vận tốc thật của cano là x
Theo đề ra, ta có PT:
4(x+2)=5(x-2)
<=>4x+8=5x-10
<=>4x-5x=-10-8
<=>-x=-18
=>x=18
Vậy vận tốc thực của cano là 18km/h
Lưu ý:v xuôi = v thực + v nước
v ngược = v thực - v nước
Câu hỏi của Nguyễn Thị Thanh Trang - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo!

Gọi vận tốc ca nô là x (km/h) , x>0
Vận tốc xuôi dòng là : x+ 2 (km/h)
Vận tốc ngược dòng là : x - 2( km/ h)
Theo đề bài ra, ta có phép tính :
( x+2).4 = (x-2).5
=> 4x+ 8 = 5x -10
=> 4x -5x = -10 -8
=> -x = -18
=> x = 18
Suy ra: vận tốc của ca nô là 18 km/h
Khoảng cách giữa 2 bến là:
(18+2).4 = 80 km
~~ hok tốt ~~

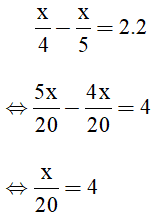
Gọi vận tốc thực của canô là x ta có
Thời gia đi xuôi dòng \(4=\frac{S}{x+2}\)=> S=4x+8
Thời gian đi ngược dòng : \(5=\frac{S}{x-2}\)=> S=5x-10
=> 4x+8=5x-10 Hay x= 18 => S=4x+8=80km
Gọi x là vận tốc thật của ca nô
Vận tốc ca nô xuôi dòng từ A đến B : x+2
Vận tốc ngược dòng từ B đến A : x-2
Khoảng cách hai bến AB tính theo vận tốc là x+2 : 4.(x+2)
Khoảng cách hai bến AB tính theo vận tốc là x-2: 5.(x-2)
Ta có pt: 4.(x+2)=5.(x-2)
<=>4x+8=5x-10
<=>x=18 (km)