Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

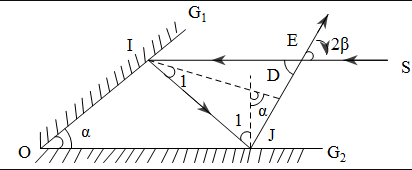
Giả sử tia tới là SI có góc tới là α độ, góc phản chiếu cũng bằng α, do hai gưong đặt vuông góc với nhau nên pháp tuyến ở guơg G1 và pháp tuyến ở guơng G2 vuông góc với nhau, tia phản xạ ở guơng G1 chính là tia tới ở guơng G2 hai góc này phụ nhau.(vẽ hình ra thấy). Ta được số đo góc tới ở guơng G2 là (90-α) độ, và góc phản chiếu = góc tới nên góc phản chiếu ở G2 = (90 - α) độ.
Tia tới ở G2 là tia IK thì từ một điểm bất kỳ M trên tia phản xạ Kt ở gưong G2 ta kẻ đừong thẳng song song với IK cắt tia SI ở H thì tứ giác HIKM là hình thoi vì có các cạnh song song với nhau và hai đường chéo vuông góc với nhau) Nên tia Kt và tia IK song song với nhau vậy góc phải tìm có giá trị bằng 0.
Có thể nói gọn thế này: pháp tuyến ở guơng G2 song với guơng G1 . Nên tia phản chiếu ở G2 cũng song song với tia tới SI ở G1.
* Kết luận là góc tạo bởi tia SI và tia phản xạ cuối cùng trên guơng G2 có giá trị bằng 0 độ.
Chúc bạn học tốt!!!
- Giả sử tia tới là SI có góc tới là α độ, góc phản chiếu cũng bằng α, do hai gưong đặt vuông góc với nhau nên pháp tuyến ở guơg G1 và pháp tuyến ở guơng G2 vuông góc với nhau, tia phản xạ ở guơng G1 chính là tia tới ở guơng G2 hai góc này phụ nhau. Ta được số đo góc tới ở guơng G2 là (90-α) độ, và góc phản chiếu = góc tới nên góc phản chiếu ở G2 = (90-α) độ.
- Tia tới ở G2 là tia IK thì từ một điểm bất kỳ M trên tia phản xạ Kt ở gưong G2 ta kẻ đừong thẳng song song với IK cắt tia SI ở H thì tứ giác HIKM là hình thoi vì có các cạnh song song với nhau và hai đường chéo vuông góc với nhau) nên tia Kt và tia IK song song với nhau vậy góc phải tìm có giá trị bằng 0.
- Có thể nói gọn thế này : pháp tuyến ở guơng G2 song với guơng G1. Nên tia phản chiếu ở G2 cũng song song với tia tới SI ở G1.
- Kết luận là góc tạo bởi tia SI và tia phản xạ cuối cùng trên guơng G2 có giá trị bằng 0 độ.
Chúc bạn học tốt!!!

Khi \(G_2\) quay một góc \(\beta\) thì tia phản xạ \(JR\) cũng quay một góc bằng nó \(\beta=60^o\)
G1 O G2 S I J R N
Xét tứ giác OINJ
có \(\widehat{O}=60^o;\widehat{I}=90^0;\widehat{J}=90^o\)
\(\Rightarrow\widehat{N}=360^o-\left(60^o+90^o+90^o\right)\)
\(\Rightarrow\widehat{N}=120^o\)
Xét \(\Delta NIJ\) \(\widehat{N}=120^o\Rightarrow\widehat{I3}+\widehat{J2}=180^o-\widehat{N}=60^o\)
\(\Rightarrow\widehat{2I3}+\widehat{2J2}=120^o\)
Xét \(\Delta IAR\)
\(\widehat{IAR}=\widehat{JIA}+\widehat{IJA}=\widehat{2I3}+\widehat{2J2}=120^o\)
Vậy \(\widehat{JAR}=120^o\)
120 độ