Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hướng dẫn giải: Ta có:
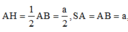
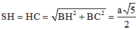
Có A H 2 + S A 2 = 5 a 2 4 = S H 2 ⇒ ∆ S A H vuông tại A
Do đó mà S A ⊥ ( A B C D ) nên
![]()
(Mặt phẳng (SAB) vuông góc với đáy (ABCD))
Trong tam giác vuông SAC, có
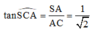

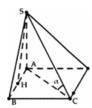
S A B C D M O N H 45 ❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)

Chọn đáp án C
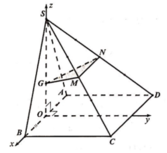
Gọi O là trung điểm AB.
Do tam giác SAB đều và nằm trong mặt phẳng vuông góc (ABCD) nên![]()
Chọn hệ trục tọa độ Oxyz như hình vẽ. Chọn a = 2.
Khi đó: ![]()
![]()
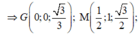
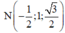
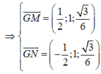
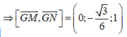
Ta có mặt phẳng (ABCD) có vecto pháp tuyến là ![]()
Mặt phẳng (GMN) có vecto pháp tuyến là 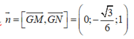
Gọi α là góc giữa hai mặt phẳng (GMN) và (ABCD)
Ta có:
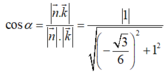
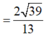

Lời giải:
Vì $(SAB), (SAD)$ cùng vuông góc với $(ABCD)$ mà $(SAB)\cap (SAD)\equiv SA$ nên $SA\perp (ABCD)$
Vì $SA\perp (ABCD)$ nên $SA\perp CB$
Mà: $AB\perp CB$
$\Rightarrow CB\perp (SAB)$
$\Rightarrow \angle (SC,(ABCD))=\angle (SC, SB)=\angle CSB=45^0$
$\Rightarrow SB=CB=a$
$SA=\sqrt{SB^2-AB^2}=\sqrt{a^2-a^2}=0$ (vô lý)
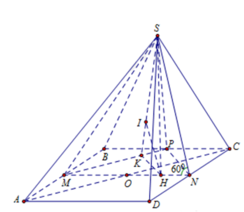
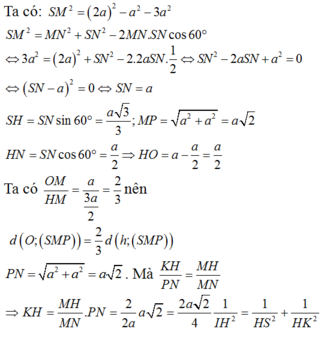
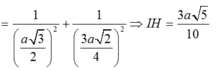
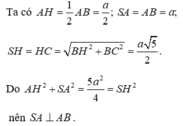


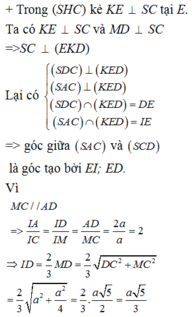


Câu 2:
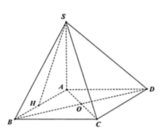
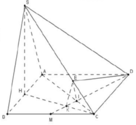
Gọi M là trung điểm AD \(\Rightarrow MH\) là đường trung bình tam giác ABD
\(\Rightarrow MH//BD\Rightarrow\) góc giữa MH và (SAD) bằng góc giữa BD và (SCD)
Trong mặt phẳng (SAB) từ H kẻ \(HP\perp SA\) (1)
\(SH\perp\left(ABCD\right)\Rightarrow SH\perp AD\)
Mà \(AD\perp AB\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp HP\) (2)
(1);(2) \(\Rightarrow HP\perp\left(SAD\right)\)
\(\Rightarrow\widehat{HMP}\) là góc giữa MH và (SAD) hay \(\widehat{HMP}=\alpha\)
\(AC=2a\sqrt{2}\Rightarrow MH=\frac{1}{2}AC=a\sqrt{2}\)
\(SH=\frac{SA\sqrt{3}}{2}=a\sqrt{3};AH=\frac{1}{2}AB=a\)
\(\frac{1}{HP^2}=\frac{1}{SH^2}+\frac{1}{AH^2}\Rightarrow HP=\frac{SH.AH}{\sqrt{SH^2+AH^2}}=\frac{a\sqrt{3}}{2}\)
\(\Rightarrow sin\alpha=\frac{HP}{MH}=\frac{\sqrt{6}}{4}\Rightarrow\alpha\approx37^045'\)
Bài 3 giống hệ bài 2, đơn giản là thu nhỏ kích thước chóp còn 1 nửa, nhưng góc ko thay đổi nên kết quả y hệt bài 2
1.
\(f'\left(x\right)=\left(m-1\right)x^2-2\left(m-1\right)x-m-4\)
Xét \(\left(m-1\right)x^2-2\left(m-1\right)x-m-4\ge0\) (1)
- Với \(m=1\) BPT vô nghiệm (ktm)
- Với \(m\ne1\) để BPT vô nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}m< 1\\\Delta'=\left(m-1\right)^2+\left(m-1\right)\left(m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 1\\\left(m-1\right)\left(2m+3\right)< 0\end{matrix}\right.\) \(\Rightarrow-\frac{3}{2}< m< 1\)
Vậy để BPT có nghiệm thì: \(\left[{}\begin{matrix}m>1\\m\le-\frac{3}{2}\end{matrix}\right.\)