Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BC=căn 3^2+4^2=5cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4
=>BD/3=CD/4=5/7
=>BD=15/7cm; CD=20/7cm

\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
c: Ta có: ΔHBA\(\sim\)ΔHAC
nên HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)
d: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
hay BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{5}{7}\)
Do đó: BD=15/7(cm); CD=20/7(cm)

a: Xét ΔABD vuông tại A và ΔECD vuông tại E có
\(\widehat{ADB}=\widehat{EDC}\)
Do đó: ΔABD\(\sim\)ΔECD

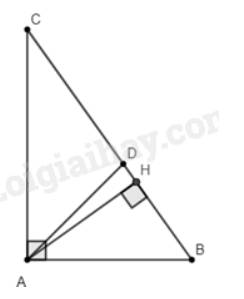
a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).

A B C 3 4 D E 5 15/7
a, Xét tam giác ABC và tam giác DEC ta có
^BAC = ^EDC = 900
^C_ chung
Vậy tam giác ABC ~ tam giác DEC ( g.g )
b, tam giác ABC vuông tại A
Áp dụng định lí Py ta go cho tam giác ABC vuông tại A ta có :
\(AB^2+AC^2=BC^2\Rightarrow BC^2=9+16=25\Rightarrow BC=5\)cm
Vì AD là tia phân giác ^A nên \(\frac{AB}{AC}=\frac{BD}{DC}\)mà DC = BC - BD = 5 - BD
\(\Rightarrow\frac{3}{4}=\frac{BD}{5-BD}\Rightarrow15-3BD=4BD\)
\(\Rightarrow7BD=15\Rightarrow BD=\frac{15}{7}\)cm
c, Ta có : \(DC=BC-BD=5-\frac{15}{7}=\frac{20}{7}\)cm
Áp dụng định lí Py ta go cho tam giác vuông tại D ta được :
\(AD^2+DC^2=AC^2\Rightarrow AD^2=AC^2-DC^2=16-\frac{400}{49}\)
\(\Rightarrow AD^2=\frac{384}{49}\Rightarrow AD=\frac{8\sqrt{6}}{7}\)xem sai ở đâu hộ mình nhé, chứ nếu theo hệ thức lượng thì như này
*\(AD.BC=AB.AC\Rightarrow AD=\frac{12}{5}\)*
d, \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.3.4=6\)