Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét ΔABC có DM//BC
nên DM/BC=AD/AB=BE/BA
Xét ΔABC có EN//BC
nên EN/BC=AE/AB
DM/BC+EN/BC=BE/AB+AE/AB=1
=>DM+EN=BC
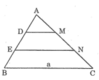
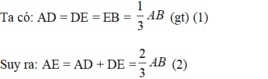
Trong ΔABC, ta có: DM // BC (gt)
Nên 
(Hệ quả định lí Ta-lét)
Suy ra : 
(3)
Từ (1) và (3) suy ra: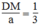 
Suy ra: 
Trong ΔABC, ta có: EN // BC (gt)
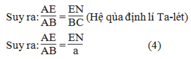
Từ (2) và (4) suy ra: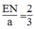 
hay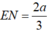 
Dựa vào tính chất đường trung bình của tam giác:
DM=EN/2
theo tính chất đương trung bình của hình thang:
EN=(DM+m)/2
1: Xét ΔABC có DE//BC
nên AE/AC=AD/AB
=>AE/8=1/3
=>AE=8/3(cm)
2:
Xét ΔABC có DE//BC
nên DE/BC=AD/AB
=>DE/10=1/3
=>DE=10/3(cm)
Xét tứ giác BDEF có
BD//EF
BF//DE
Do đó: BDEF là hình bình hành
=>BF=DE=10/3(cm)
3:
AD/AB=1/3
AE/AC=1/3
DE/BC=1/3
Do đó: AD/AB=AE/AC=DE/BC
Xét ΔABC có DE//BC
nên \(\dfrac{AD}{AB}=\dfrac{DE}{BC}\)
=>\(\dfrac{DE}{8}=\dfrac{2}{5}\)
=>\(DE=2\cdot\dfrac{8}{5}=\dfrac{16}{5}=3,2\left(cm\right)\)
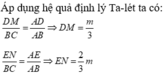
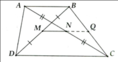
A B C D E M N 1 1 1 F 1
Trên BC lấy F sao cho BF=EN
Vì EN//BC nên ENFB là hình thang
Mà BF=EN nên EB//NF;EB=NF
=>B1=F1
Vì DM//BC nên D1=B1
Do đó F1=D1(=B1)
Vì BE=AD mà BE=FN nên AD=FN
Ta có BAC=180-B-C
FNC=180-F1-C
=>BAC=FNC
Xét tam giácADM và tam giácNFC ta có:
BAC=FNC;AD=NF; F1=D1
Do đó tam giácADM = tam giácNFC
=>DM=FC
Ta có BC=FC+BF=DM+EN(đpcm)