Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Vì `MI bot BC`
`=>hat{MIC}=90^o`
`HM bot HC`
`=>hat{MHC}=90^o`
`=>hat{MHC}+hat{MIC}=180^o`
`=>` tg HMIC nt
b)Vì HMIC nt
`=>hat{HCM}=hat{MIH}`
Mà `hat{HCM}=hat{MBC}`(góc nt và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung MC nhỏ)
`=>hat{MIH}=hat{MCB}`
Đoạn còn lại thì mình không biết điểm F ở đâu ker

1) Hình vẽ câu 1) đúng
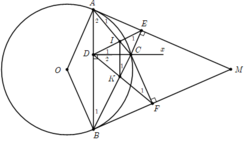
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

Gọi H là hình chiếu của O trên BC.
ta có OH = const (BC cố định)
a.
{MI ⊥ABMK ⊥AC{MI ⊥ABMK ⊥AC
→{AIM^=90oAKM^=90o→{AIM^=90oAKM^=90o
→→ tứ giác AIMK nt đtròn đkính AM.
b.
Ta có:
MKC^+MPC^=180oMKC^+MPC^=180o
→→ Tứ giác MPCK nt đtròn đkính MC
→MPK^=MCK^ (1)→MPK^=MCK^ (1) (góc nt cùng chắn MK⌢MK⌢ )
Xét (O;R), ta có:
MBC^=MCK^ (2)MBC^=MCK^ (2) (góc nt và góc tt với dây cung cùng chắn MC⌢MC⌢ )
K/h (1),(2) : MPK^=MBC^ (3)MPK^=MBC^ (3)
c. lần lượt CM:
MPK^=MIP^ (4)MPK^=MIP^ (4)
MPI^=MKP^MPI^=MKP^
→ΔMIP∼ΔMPK→ΔMIP∼ΔMPK
Tỉ số đồng dạng :
MIMP=MPMKMIMP=MPMK
→MP2=MI.MK→MP2=MI.MK
→MP3=MI.MK.MP→MP3=MI.MK.MP
MI.MK.MPMax↔MPMaxMI.MK.MPMax↔MPMax
Ta có: MP+OH≤RMP+OH≤R
→MP≤R−OH→MP≤R−OH
→MPMax→MPMax bằng R-OH. Khi O,H,M thẳng hàng
Vậy MI.MK.MPMax=(R−OH)3MI.MK.MPMax=(R−OH)3 khi O,H,M thẳng hàng

a: Xét tứ giác AIMK có
góc AIM+góc AKM=180 độ
=>AIMK là tứ giác nội tiếp
b: Xet tứ giác CPMK có
góc CPM+góc CKM=180 độ
=>CPMK là tứ giac nội tiếp
=>góc MPK=góc MCK
góc MBC=góc MBP=góc MIP
mà góc MIP=góc MCK
nên góc MPK=góc MBC

Gọi H là hình chiếu của O trên BC.
ta có OH = const (BC cố định)
a.
{MI ⊥ABMK ⊥AC{MI ⊥ABMK ⊥AC
→{AIM^=90oAKM^=90o→{AIM^=90oAKM^=90o
→→ tứ giác AIMK nt đtròn đkính AM.
b.
Ta có:
MKC^+MPC^=180oMKC^+MPC^=180o
→→ Tứ giác MPCK nt đtròn đkính MC
→MPK^=MCK^ (1)→MPK^=MCK^ (1) (góc nt cùng chắn MK⌢MK⌢ )
Xét (O;R), ta có:
MBC^=MCK^ (2)MBC^=MCK^ (2) (góc nt và góc tt với dây cung cùng chắn MC⌢MC⌢ )
K/h (1),(2) : MPK^=MBC^ (3)MPK^=MBC^ (3)
c. lần lượt CM:
MPK^=MIP^ (4)MPK^=MIP^ (4)
MPI^=MKP^MPI^=MKP^
→ΔMIP∼ΔMPK→ΔMIP∼ΔMPK
Tỉ số đồng dạng :
MIMP=MPMKMIMP=MPMK
→MP2=MI.MK→MP2=MI.MK
→MP3=MI.MK.MP→MP3=MI.MK.MP
MI.MK.MPMax↔MPMaxMI.MK.MPMax↔MPMax
Ta có: MP+OH≤RMP+OH≤R
→MP≤R−OH→MP≤R−OH
→MPMax→MPMax bằng R-OH. Khi O,H,M thẳng hàng
Vậy MI.MK.MPMax=(R−OH)3MI.MK.MPMax=(R−OH)3 khi O,H,M thẳng hàng

Bài 1:
Đề bài: Cho đường tròn (�;�)(O;R) và điểm �A nằm ngoài đường tròn. Từ điểm �A kẻ hai tiếp tuyến ��AB, ��AC với đường tròn (�,�)(B,C) là các tiếp điểm. Trên cung nhỏ ��BC lấy một điểm �M tùy ý (mà �M không trùng với �B và �C), kẻ ��MI vuông góc với ��AB, ��MK vuông góc với ��AC, ��MP vuông góc với ��BC (với �∈��I∈AB, �∈��K∈AC, �∈��P∈BC).
b) Chứng minh rằng: ��⋅��=��2MI⋅MK=MP2.
a) Chứng minh rằng: Tứ giác ����AIMK là tứ giác nội tiếp đường tròn.
Giải thích và chứng minh:
Phần b): Chứng minh rằng ��⋅��=��2MI⋅MK=MP2
Vị trí các điểm và thiết lập ban đầu:
Các đoạn vuông góc:
Dựng các tam giác vuông:
Sử dụng định lý tiếp tuyến:
Phần a): Chứng minh rằng tứ giác ����AIMK là tứ giác nội tiếp đường tròn
Định lý tứ giác nội tiếp:
Các góc cần xét:
Sử dụng định lý các góc tiếp tuyến:
Kết luận:
Kết luận: