Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có:
\(49^x-35^x-25^x=0\)
\(\Leftrightarrow \frac{49^x}{25^x}-\frac{35^x}{25^x}-1=0\)
\(\Leftrightarrow \left(\frac{7}{5}\right)^{2x}-\left(\frac{7}{5}\right)^x-1=0\)
Đặt \(\left(\frac{7}{5}\right)^x=t\Rightarrow t^2-t-1=0\)
Ta thấy \(\Delta=5>0\Rightarrow t^2-t-1=0\) có hai nghiệm phân biệt
Theo hệ thưc Viete với $t_1,t_2$ là hai nghiệm của pt thì \(t_1t_2=-1<0 \) , do đó pt có hai nghiệm trái dấu. Vì $t>0$ nên chỉ có một nghiệm thỏa mãn.
Chỉ có một $t$ thỏa mãn đồng nghĩa với việc chỉ có một giá trị $x$ thỏa mãn
Vậy phương trình ban đầu có một nghiệm.

a. 32x - 5.(3.2)x + 22x.4 =0
(=) \(\left(\dfrac{3}{2}\right)^{^{2x}}-5.\left(\dfrac{3}{2}\right)^x+2^{2x}.4\) =0
đặt \(\left(\dfrac{3}{2}\right)^x=t\) đk: t > 0
=> pttt: t2 - 5t +4 =0
(=)\(\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\)
(=) \(\left[{}\begin{matrix}\left(\dfrac{3}{2}\right)^x=1\\\left(\dfrac{3}{2}\right)^x=4\end{matrix}\right.\)
(=)\(\left[{}\begin{matrix}x=0\\x=\log_{\dfrac{3}{2}}4\end{matrix}\right.\)
b. 3.52x + 2.72x - 5.(5.7)x =0
(=) \(3+2.\left(\dfrac{7}{5}\right)^{2x}-5.\left(\dfrac{7}{5}\right)^x=0\)
đặt \(t=\left(\dfrac{7}{5}\right)^x\) đk: t > 0
pttt: 3+2t2-5t=0
(=) \(\left[{}\begin{matrix}t=1\\t=\dfrac{3}{2}\end{matrix}\right.\)
(=)\(\left[{}\begin{matrix}x=0\\x=\log_{\dfrac{7}{5}}\dfrac{3}{2}\end{matrix}\right.\)

Ta có : \(\left(a^{\log_37}\right)^{\log_37}+\left(b^{\log_711}\right)^{\log_711}+\left(c^{\log_{11}25}\right)^{\log_{11}25}=27^{^{\log_37}}+49^{^{\log_711}}+\left(\sqrt{11}\right)^{^{\log_{11}25}}\)
\(=7^3+11^2+25^{\frac{1}{2}}=469\)

\(G=lg\left(25^{\log_56}+49^{\log_78}\right)-e^{\ln3}=lg\left[\left(5^2\right)^{\log_56}+\left(7^2\right)^{\log_78}\right]-3\)
\(=lg\left(5^{\log_56^2}+7^{\log_78^2}\right)-3\)
\(=lg\left(6^2+8^2\right)-3=lg10^{2-3}=2-3=-1\)

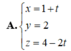
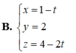
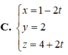
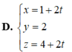




Giải:
a, 27 + 46 + (-79) + 54 + (-21)
= 27 + (46 + 54) - (79 + 21)
= 27 + 100 - 100
= 27
b, -25.72 + 25.21 - 49.25
= 25(-72 + 21 - 49)
= 25.(-100)
= -2500
c, 35(14 -23) - 23(14 - 35)
= 35.14 - 35.23 - 23.14 + 23.35
= (35.14 - 23.14) - (35.23 - 23.35)
= 14(35 - 23) - 0
= 14.12
= 168
d, -25.21 + 25.72 + 49.25
= 25(-21 + 72 + 49)
= 25.100
= 2500
e, -1911 - (1234 - 1911)
= -1911 - 1234 + 1911
= (1911 - 1911) - 1234
= -1234
g, 156.72 + 28.156
= 156(72 + 28)
= 156.100
= 15600
Chúc bạn học tốt !