Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi vận tốc của BT là x (km/h)(x>0)
gọi vận tốc của CBN là y (km/h) (y>0)
vì hai người gặp nhau khi BT đi đc 1h30` = 1,5h nên quãng đường của BT đi là 1,5/x (km)
CBN đi là 2/y (km)
vì làng và thị xã cách nhau 38 km nên ta có 1,5/x + 2/y = 38 (1)
sau 1h15` = 5/4h , BT đi đc 5x/4 (km)
CBN đi đc 5y/4 (km)
vì sau 5/4h thì hai người cách nhau 10,5km nên ta có 5x/4 + 5y/4 =27,5 (2)
từ (1) và (2) ta có hệ phương trình
bn tự giải hệ nha , kết quả là x= 12;y=10

Tham khảo ạ ~
Gọi vận tốc của bác Hòa là x (x>0; km/h)
vận tốc của cô Liên là y (y>0; km/h)
Đổi: 1h30p=1,5h
2 người gặp nhau khi bác Hòa đi được 2h, cô Liên đi được 3h nên ta có pt:
2x+3y=54 (1)
2 người khởi hành đồng thời và cách nhau 21km sau 1h30p, ta có pt:
1,5x+1,5y= 54-21
=> x+y=22(2)
Từ (1) và (2) ta có hệ pt:


Đặt vận tốc của người đi từ A là vA và vận tốc của người đi từ B là vB. Theo đề bài, khi người đi từ A đã đi 1,5h và người đi từ B đã đi 2h thì họ gặp nhau. Tổng quãng đường mà người đi từ A và người đi từ B đã đi trong khoảng thời gian này là 30km (khoảng cách giữa A và B). Từ đó, ta có phương trình sau: 1,5vA + 2vB = 30 (1) Tiếp tục, khi 2 người đi từ A và Khởi động đồng thời, sau 1h15p (tức là 1,25h), họ còn cách nhau 10 ,5km. Ta có phương trình sau: (vA + vB) * 1,25 = 10,5 (2) Giải hệ phương trình (1) và (2) để tính toán vận tốc của mỗi người đi. Với (1): 1,5vA + 2vB = 30 Nhân cả hai mắt của phương trình cho 2: 3vA + 4vB = 60 (3) Với (2): (vA + vB) * 1,25 = 10,5 vA + vB = 8,4 (4) Giải hệ phương trình (3) và (4) để tìm giá trị của vA và vB. Từ (3), ta có: vA = 60 - 4vB (5) Thay (5) vào (4), ta được phương trình chỉ chứa một biến số vB: (60 - 4vB) + vB = 8,4 60 - 3vB = 8,4 -3vB = -51,6 vB = 17,2 Thầy vB = 17,2 vào (5), ta có: vA = 60 - 4(17,2) vA = 60 - 68,8 vA = - 8,8 Vì vận tốc không thể phát ra âm thanh, nên bỏ qua giá trị vA = -8,8 và kết luận rằng vận tốc không thể tính được của người đi từ A và B trong trường hợp này

Gọi vận tốc của xe máy là x (km/h), xe đạp y (km/h) (x,y>0)
40 phút = \(\frac{2}{3}\)giờ
Quãng đường xe máy đi là \(\frac{2}{3}\times x\)
Quãng đường xe đạp đi là \(\frac{2}{3}\times y\)
Vì họ gặp nhau nếu đi ngược chiều nên:
\(\frac{2}{3}\times x+\frac{2}{3}\times y=30\)
\(\Rightarrow x+y=45\left(1\right)\)
Nếu đi cùng chiều thì sau 2h xe máy đuổi kịp xe đạp nên ta có:
\(2x-2y=AB=30\)
\(\Rightarrow x-y=15\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow\hept{\begin{cases}x+y=45\\x-y=15\end{cases}\Rightarrow\hept{\begin{cases}x=30\\y=15\end{cases}}}\)
Vậy vận tốc mỗi xe là 30 km/h và 15 km/h

Gọi vận tốc xe của cô Liên là x (km/h, x > 0).
⇒ Vận tốc xe của bác Hiệp là: x + 3 (km/h).
Thời gian bác Hiệp, cô Liên đi là: 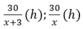
Thời gian đi của bác Hiệp ít hơn thời gian đi của cô Liên là nửa giờ nên ta có phương trình:
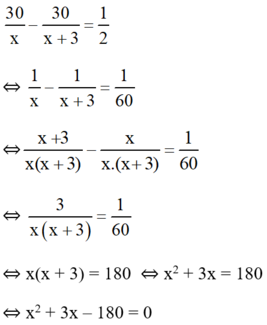
Có a = 1; b = 3; c = -180 ⇒ Δ = 32 – 4.1.(-180) = 729
Phương trình có hai nghiệm:
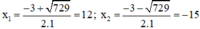
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy vận tốc của cô Liên là 12km/h, của bác Hiệp là 15 km/h.

Gọi vận tốc xe của cô Liên là x (km/h, x > 0).
⇒ Vận tốc xe của bác Hiệp là: x + 3 (km/h).
Thời gian bác Hiệp, cô Liên đi là: 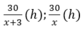
Thời gian đi của bác Hiệp ít hơn thời gian đi của cô Liên là nửa giờ nên ta có phương trình:
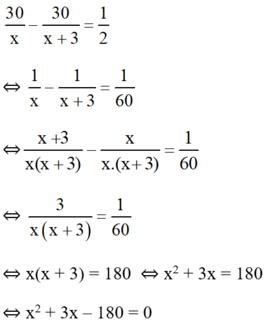
Có a = 1; b = 3; c = -180 ⇒ Δ = 3 2 – 4 . 1 . ( - 180 ) = 729
Phương trình có hai nghiệm:
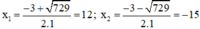
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy vận tốc của cô Liên là 12km/h, của bác Hiệp là 15 km/h.

Gọi x, y (km/h) lần lượt là vận tốc của bác Toàn và cô ba Ngần đi. Điều kiện: x > 0, y > 0.
Vì hai người đi ngược chiều nhau, bác Toàn đi 1 giờ 30 phút, cô ba Ngần đi 2 giờ thì gặp nhau và tổng quãng đường họ đi được bằng khoảng cách từ làng đến thị xã nên ta có phương trình: 1,5x + 2y = 38
Quãng đường bác Toàn đi trong 1 giờ 15 phút là: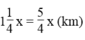
Quãng đường cô ba Ngần đi trong 1 giờ 15 phút là: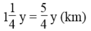
Sau 1 giờ 15 phút, hai người còn cách nhau 10,5km nên ta có phương trình:
⇔ 5x + 5y = 110
Ta có hệ phương trình:
Giá trị của x và y thỏa điều kiện bài toán.
Vậy vận tốc của bác Toàn là 12km/h, vận tốc của cô ba Ngần là 10km/h.