Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết suy ra xác suất để người thứ nhất, thứ hai, thứ ba bắn không trúng đích lần lượt là 0,5; 0,4 và 0,2
Để có đúng người bắn trúng đích thì có các trường hợp sau
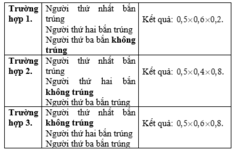
Vậy xác suất để có đúng người bắn trúng đích là
![]()
Chọn B.

Đáp án D
Phương pháp:
A, B là các biến cố độc lập thì P ( A . B ) = P ( A ) . P ( B )
Chia bài toán thành các trường hợp:
- Một người bắn trúng và một người bắn không trúng,
- Cả hai người cùng bắn không trúng.
Sau đó áp dụng quy tắc cộng.
Cách giải:
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 − 1 2 = 1 2 .
Xác suất để xạ thủ thứ nhất bắn không trúng bia là: 1 − 1 3 = 2 3 .
Gọi biến cố A:”Có ít nhất một xạ thủ không bắn trúng bia ”.
Khi đó biến cố A có 3 khả năng xảy ra:
+) Xác suất người thứ nhất bắn trúng bia, người thứ hai không bắn trúng bia: 1 2 . 2 3 = 1 3 .
+) Xác suất người thứ nhất không bắn trúng bia, người thứ hai bắn trúng bia: 1 2 . 1 3 = 1 6 .
+) Xác suất cả hai người đều bắn không trúng bia:
Khi đó P ( A ) = 1 2 . 2 3 + 1 2 . 1 3 + 1 2 . 1 3 = 2 3 .

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm



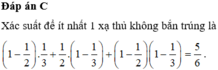
Chọn B