Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(5+\left(-7\right)+9+\left(-11\right)+13+\left(-15\right)\)
\(=\left[5+\left(-7\right)\right]+\left[9+\left(-11\right)\right]+\left[13+\left(-15\right)\right]\)
\(=\left(-2\right)+\left(-2\right)+\left(-2\right)=-6\)
b)
\(\left(-6\right)+8+\left(-10\right)+12+\left(-14\right)+16\)
\(=\left[\left(-6\right)+8\right]+\left[\left(-10\right)+12\right]+\left[\left(-14\right)+16\right]\)
\(=2+2+2=6\)

a) \(1+\left(-3\right)+5+\left(-7\right)+9+\left(-11\right)\\ =\left(1+5+7\right)-\left(3+7+11\right)\\ =14-21\\ =-7\)
b) \(\left(-2\right)+4+\left(-6\right)+8+\left(-10\right)+12\\ =\left(4+8+12\right)-\left(2+6+10\right)\\ =24-18\\ =6\)

a, \(\left(-6\right)+\left(-3\right).....\left(-6\right)\)
\(\left(-9\right)< \left(-6\right)\)
Vậy \(\left(-6\right)+\left(-3\right)< \left(-6\right)\)
b,\(\left(-9\right)+\left(-12\right)....\left(-20\right)\)
\(\left(-21\right)< \left(-20\right)\)
\(\Rightarrow\left(-9\right)+\left(-12\right)< \left(-20\right)\)

a) (-2)+ (-5) = -7
Vì: -7< -5
=> (-2)+ (-5) < -7
b) (-3)+ (-8)= -11
Vì: (-10) > (-11)
=> -10> (-3)+ (-8)

\(7-\left\{12-\left[-\left(-3\right)+\left(-10\right)-\left(-11\right)\right]-\left[-\left(-9\right)+\left(-8\right)-12\right]\right\}\)\(-\left(-4\right)\)
= \(7-\left\{12-\left[3+\left(-10\right)+11\right]-\left[9+\left(-8\right)-12\right]\right\}\) \(+4\)
= \(7-\left\{12-\left[7+11\right]-\left[1-12\right]\right\}+4\)
= \(7-\left\{12-18-\left(-11\right)\right\}+4\)
= \(7-\left\{-6+11\right\}+4\)
= \(7-5+4\)
= 6
7 - { 12 - [ - (- 3) + (- 10) - (- 11) ] - [ - (- 9) + (- 8) - (+ 12) ] } - (- 4)
= 7 - [ 12 - ( 3 - 10 + 11 ) - ( 9 - 8 - 12 ) ] + 4
= 7 - ( 12 - 4 + 11 ) + 4
=7 - 19 + 4
= - 8

a) Đặt \(A=\left(10^2+11^2+12^2\right)\div\left(13^2+14^2\right)\)
- Ta có: \(A=\left(100+121+144\right)\div\left(169+196\right)\)
\(\Leftrightarrow A=365\div365=1\)
Vậy \(A=1\)
b) Đặt \(B=1.2.3.....9-1.2.3.....8-1.2.3.....8^2\)
- Ta có: \(B=1.2.3.....8.\left(9-1\right)-1.2.3.....8^2\)
\(\Leftrightarrow B=1.2.3.....8.8-1.2.3.....8.8=0\)
Vậy \(B=0\)
c) Đặt \(C=\frac{\left(3.4.2^{16}\right)^2}{11.2^{13}.4^{11}-16^9}\)
- Ta có: \(C=\frac{3^2.4^2.2^{32}}{11.2^{13}.2^{22}-2^{36}}\)
\(\Leftrightarrow C=\frac{3^2.2^4.2^{32}}{11.2^{35}-2^{36}}\)
\(\Leftrightarrow C=\frac{3^2.2^{36}}{2^{35}.\left(11-2\right)}\)
\(\Leftrightarrow C=\frac{9.2^{36}}{2^{35}.9}\)
\(\Leftrightarrow C=2\)
Vậy \(C=2\)
d) Đặt \(D=1152-\left(374+1152\right)+\left(-65+374\right)\)
- Ta có: \(D=1152-374-1152-65+374\)
\(\Leftrightarrow D=\left(1152-1152\right)+\left(374-374\right)-65\)
\(\Leftrightarrow D=-65\)
Vậy \(D=-65\)

\(a,\dfrac{121.75.130.169}{39.60.11.198}=\dfrac{11.11.25.3.13.10.169}{13.3.6.10.11.11.18}=\dfrac{25.169}{6.18}\)

a) (-24) + 6 + 10 + 24
= [(-24) + 24] + 6 + 10
= 0 + 6 + 10
= 16
b) 15 + 23 + (-25) + (-23)
= [15+ (-25)] + [23 +(-23)]
= -10 + 0
= -10
c) (-3) + (-350) + (-7) + 350
=[-350 + 350] + [-3+(-7)]
= 0 + (-10)
= -10
d) (-9) + (-11) +21 + (-1)
= [ (-9) + (-11) ] + [ 21 + (-1)]
= -20 + 20
= 0
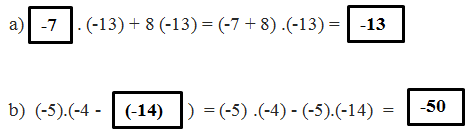
a)( -11) .(8.9)= (-11) .8 - (-11) .9= 11
b) (-12).10 - (-9) . 10= [ -12 - (-9) ] . 10 = -30
a) \(\left(-11\right)\cdot\left(8-9\right)=\left(-11\right)\cdot8-\left(-11\right)\cdot9=11\)
b) \(\left(-12\right)\cdot10-\left(-9\right)\cdot10=\left[-12-\left(-9\right)\right]\cdot10=-30\)