Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

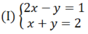
Trừ từng vế hai phương trình của hệ (I) ta được phương trình:
(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1
Khi đó, ta thu được hệ phương trình mới:
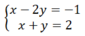
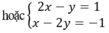

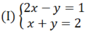
Trừ từng vế hai phương trình của hệ (I) ta được phương trình:
(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1
Khi đó, ta thu được hệ phương trình mới:
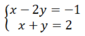
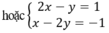

Gọi số cần tìm là ab (đk)
Theo đề bài ta có hpt:
\(\hept{\begin{cases}10a+b=a^2+b^2-11\\10a+b=2ab+5\end{cases}}\)\(\Rightarrow2ab+5=a^2+b^2-11\)
\(\Leftrightarrow a^2+b^2-2ab=16\)
\(\Leftrightarrow\left(a-b\right)^2=16\Rightarrow\orbr{\begin{cases}a-b=4\\a-b=-4\end{cases}}\)
TH1: Nếu a = b+4\(\Rightarrow10\left(b+4\right)+b=2\left(b+4\right)b+5\)
\(\Leftrightarrow3b+35-2b^2=0\)\(\Leftrightarrow\left(7+2b\right)\left(b-5\right)=0\Rightarrow b=5\Rightarrow a=9\)
TH2: Nếu a = -4+b\(\Rightarrow10\left(-4+b\right)+b=2\left(b-4\right)b+5\)
\(\Leftrightarrow-45+19b-2b^2=0\Leftrightarrow\left(b-5\right)\left(-2b+9\right)=0\)\(\Rightarrow b=5\Rightarrow a=1\)
Vậy số cần tìm là 95 và 15

b: \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=6x-1=3-1=2\end{matrix}\right.\)

Đáp ứng yêu cầu luôn
\(\hept{\begin{cases}3,3x+4,2y=1\\9x+14y=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-29,7x-37,8y=-9\\29,7x+46,2y=13,2\end{cases}}\)
Lấy trên cộng dưới (dùng cộng đại số rồi đấy)
\(\hept{\begin{cases}9x+14y=4\\8,4y=4,2\end{cases}}\)
\(\hept{\begin{cases}y=\frac{1}{2}\\x=-\frac{1}{3}\end{cases}}\)

Cả hai à tham thế i:
Cộng Đại Số
\(\hept{\begin{cases}8x-7y=5\\12x+13y=-8\end{cases}\Leftrightarrow\hept{\begin{cases}24x-21y=15\left(1\right)\\24x+26y=-16\left(2\right)\end{cases}}}\)
Lấy (2) trừ (1)
\(\left(24x-24x\right)-21y-26y=15-\left(-16\right)\)
\(\Leftrightarrow47y=-31\Rightarrow y=\frac{31}{47}\)thay vào đầu x=5+7.31/47

\(\hept{\begin{cases}-0,5x+1,2y=2,7\\x-4,5y=-7,5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}-x+2,4y=5,4\\x-4,5y=-7,5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x-4,5y=-7,5\\-21y=-2,1\\x=4,5y-7,5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=1\\x=-3\end{cases}}\)
\(\hept{\begin{cases}-0,5x+1,2y=2,7\\x-4,5y=7,5\end{cases}}\) <=> \(\hept{\begin{cases}-0,5x+1,2y=2,7\\0,5x-2,25y=3,75\end{cases}}\) <=> \(\hept{\begin{cases}-0,5x+1,2y=2,7\\-1,05y=6,45\end{cases}}\) <=> \(\hept{\begin{cases}x=\frac{1,2y-2,7}{0,5}=\frac{1,2.-\frac{43}{7}-2,7}{0,5}=-\frac{141}{7}\\y=-\frac{43}{7}\end{cases}}\)
Vậy nghiệm của hpt là: \(\left(-\frac{141}{7};-\frac{43}{7}\right)\)
Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được: 5y = 5
Do đó
Vậy hệ phương trình có nghiệm duy nhất (7/2;1)