Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(P=\dfrac{a+3}{a}\cdot\dfrac{a^2-9-6a+18}{\left(a-3\right)\left(a+3\right)}\)
\(=\dfrac{\left(a-3\right)^2}{a\left(a-3\right)}=\dfrac{a-3}{a}\)
b: Để P=-2 thì -2a=a-3
=>-3a=-3
=>a=1
c: Để P nguyên thì a-3 chia hết cho a
=>-3 chia hết cho a
mà a<>0; a<>3; a<>-3
nên \(a\in\left\{1;-1\right\}\)

a) \(\left(a+b\right)^3-\left(a-b\right)^3-6a^2b\)
\(\Leftrightarrow a^3+3a^2b+3ab^2+b^3-\left(a^3-3a^2b+3ab^2-b^3\right)-6a^2b\)
\(\Leftrightarrow a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3-6a^2b\)
\(\Leftrightarrow2b^3\)
b) \(\left(a+b\right)^3-\left(a-b\right)^3-6ab^2\)
\(\Leftrightarrow a^3+3a^2b+3ab^2+b^3-\left(a^3-3a^2b+3ab^2-b^3\right)-6ab^2\)
\(\Leftrightarrow a^3+3a^2b+3ab^2+b^3-a^3+3a^2b-3ab^2+b^3-6ab^2\)
\(\Leftrightarrow2b^3+6a^2b-6ab^2\)

\(\left(x+2\right)\left(x-2\right)-\left(x+2\right)^2\)
\(=\left(x+2\right)\left(x-2-x-2\right)\)
\(=\left(-4\right)\left(x+2\right)\)

\(A-1=\left(x+1\right)\left(x^2+1\right)...\left(x^{256}+1\right)\)
\(\Rightarrow\left(A-1\right)\left(x-1\right)=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)...\left(x^{256}+1\right)\)
\(\Rightarrow\left(A-1\right)\left(x-1\right)=\left(x^2-1\right)\left(x^2+1\right)...\left(x^{256}+1\right)\)
\(\Rightarrow\left(A-1\right)\left(x-1\right)=\left(x^4-1\right)\left(x^4+1\right)...\left(x^{256}+1\right)\)
\(\Rightarrow\left(A-1\right)\left(x-1\right)=\left(x^{256}-1\right)\left(x^{256}+1\right)=x^{512}-1\)
\(\Rightarrow A-1=\dfrac{x^{512}-1}{x-1}\)
\(\Rightarrow A=\dfrac{x^{512}-1}{x-1}+1=\dfrac{x^{512}+x-2}{x-1}\)
rut gon bieu thuc :
\(\left(x+1\right)^4-6\left(x+1\right)^2-\left(x^2-2\right).\left(x^2+2\right)\)

\(\left(x+1\right)^4-6\left(x+1\right)^2-\left(x^2-2\right)\left(x^2+2\right)\\ =x^4+4x^3+6x^2+4x+1-6x^2-12x-6-x^4+4\\ =4x^3-8x+5\)
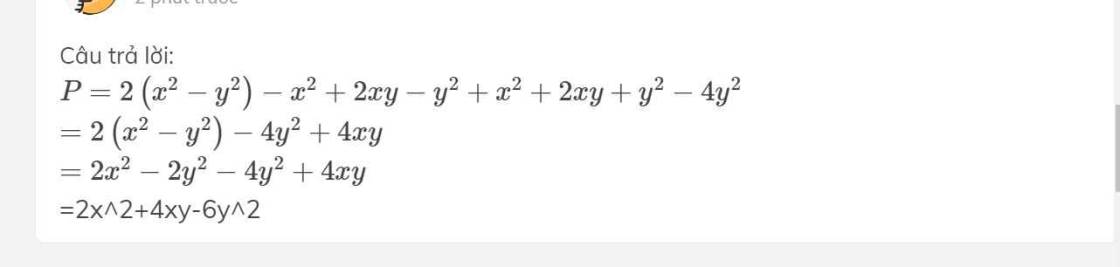
\(\left(a+b-c\right)^2-\left(a-c\right)^2-2ab+2bc\)
\(=a^2+b^2+c^2+2ab-2ac-2bc-a^2+2ac-c^2-2ab+2bc\)
\(=b^2\)
ko biết